Question

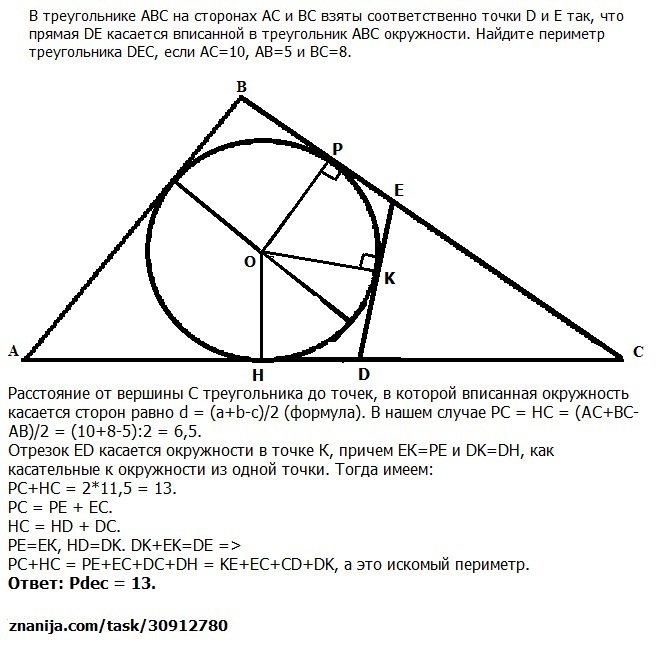
В треугольнике ABC на сторонах AС и BC взяты соответственно точки D и E так, что прямая DE касается вписанной в треугольник ABC окружности. Найти периметр треугольника DEC, если AC = 10, AB = 5, BC = 8.

Answer 1

Расстояние от вершины С треугольника до точек, в которой вписанная окружность касается сторон равно d = (a+b-c)/2 (формула). В нашем случае РС = НС = (АС+ВС-АВ)/2 = (10+8-5):2 = 6,5 ед.

Отрезок ED касается окружности в точке К, причем ЕК=РЕ и DK=DH, как касательные к окружности из одной точки. Тогда имеем:

PC+HC = 2*11,5 = 13.

РС = РЕ + ЕС.

НС = НD + DС.

РЕ=ЕК, HD=DK. DK+EK=DE =>

PC+HC = РЕ+EC+DC+DH = KE+EC+CD+DK, а это искомый периметр.

Ответ: Рdec = 13.

Answer 2

Если Вам не сложно...Помогите мне тоже, пожалуйста.... Я что-то туплю....Очень Вас прошу...https://znanija.com/task/30919401