Точка О-центр правильного треугольника АВС сторона которого равна 6 см. Прямая МА перпендикулярна плоскости АВС. Найдите угол между прямой МО и плоскостью АВС, если МА=2см.
Ответы
Ответ дал:
0
Отрезок АО - радиус описанной окружности для равностороннего треугольника, он равен а/√3 = 6/√3=2√3.
Значит из треугольника АОМ находим угол АОМ по его тангенсу tgAOM=2/(2√3)= 1/√3. Угол 30 градусов.
Приложения:
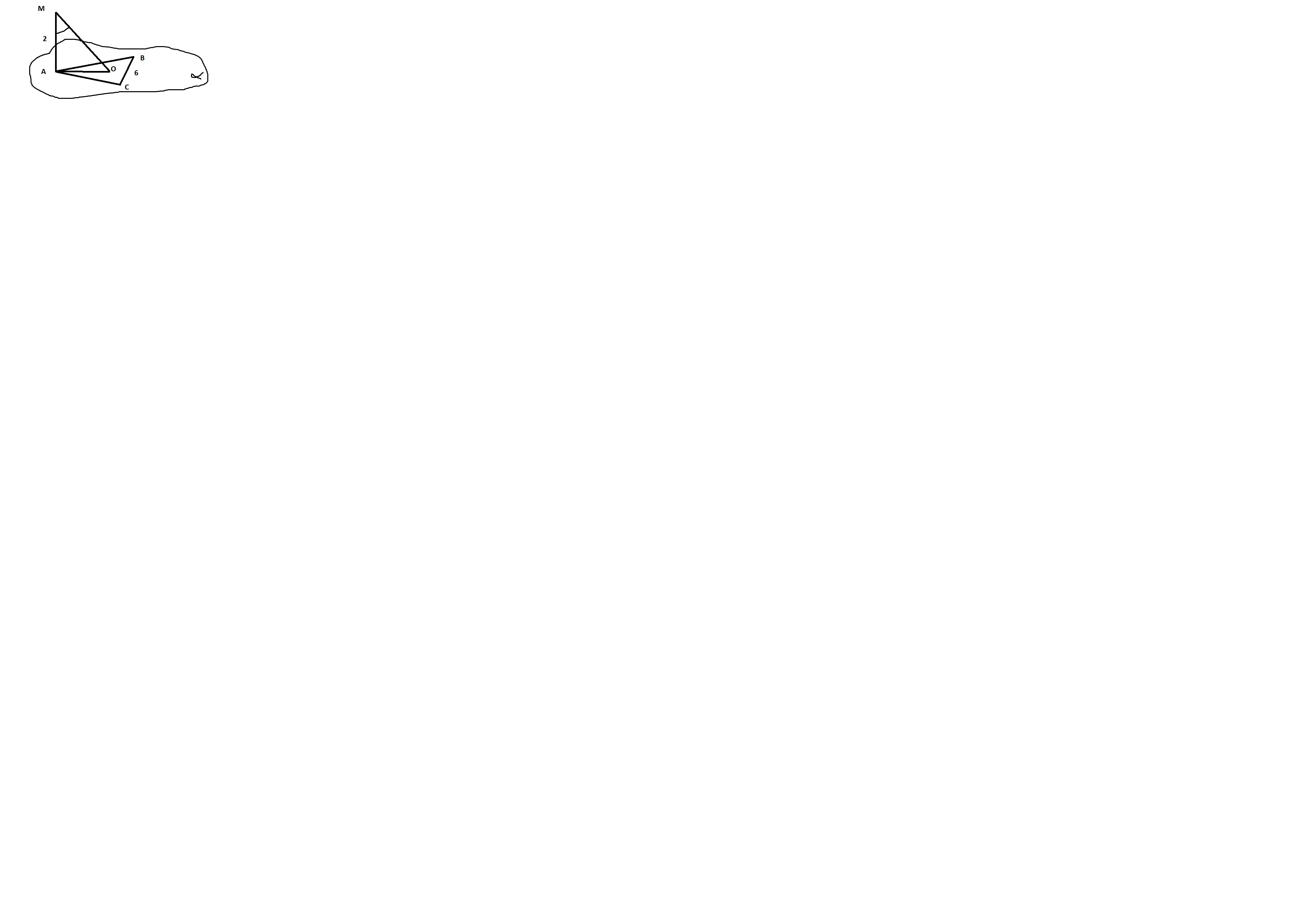
Ответ дал:
0
ДА ГДЕ ВЫ ВСЕ БЕРЕТЕ ТАНГЕНС 1√3?!
Ответ дал:
0
Чертим тр-к АВС, проводим медиану(она же высота) АН вэтом тр-ке, проводим прямую МА перпендикулярно АВС, соединяем тМ с т. О, которая лежит на АН, АО=2/3 АН, по св-ву медиан тр-ка. АН=6V3/2, тогда АО= 2/3*6V3/2=2V3, угол между прямой и пл-ю это уголМОА, из тр-ка МОА: tg<МОА=АМ/АО=2:2V3=1/V3, значит <МОА=30 гр.
Приложения:
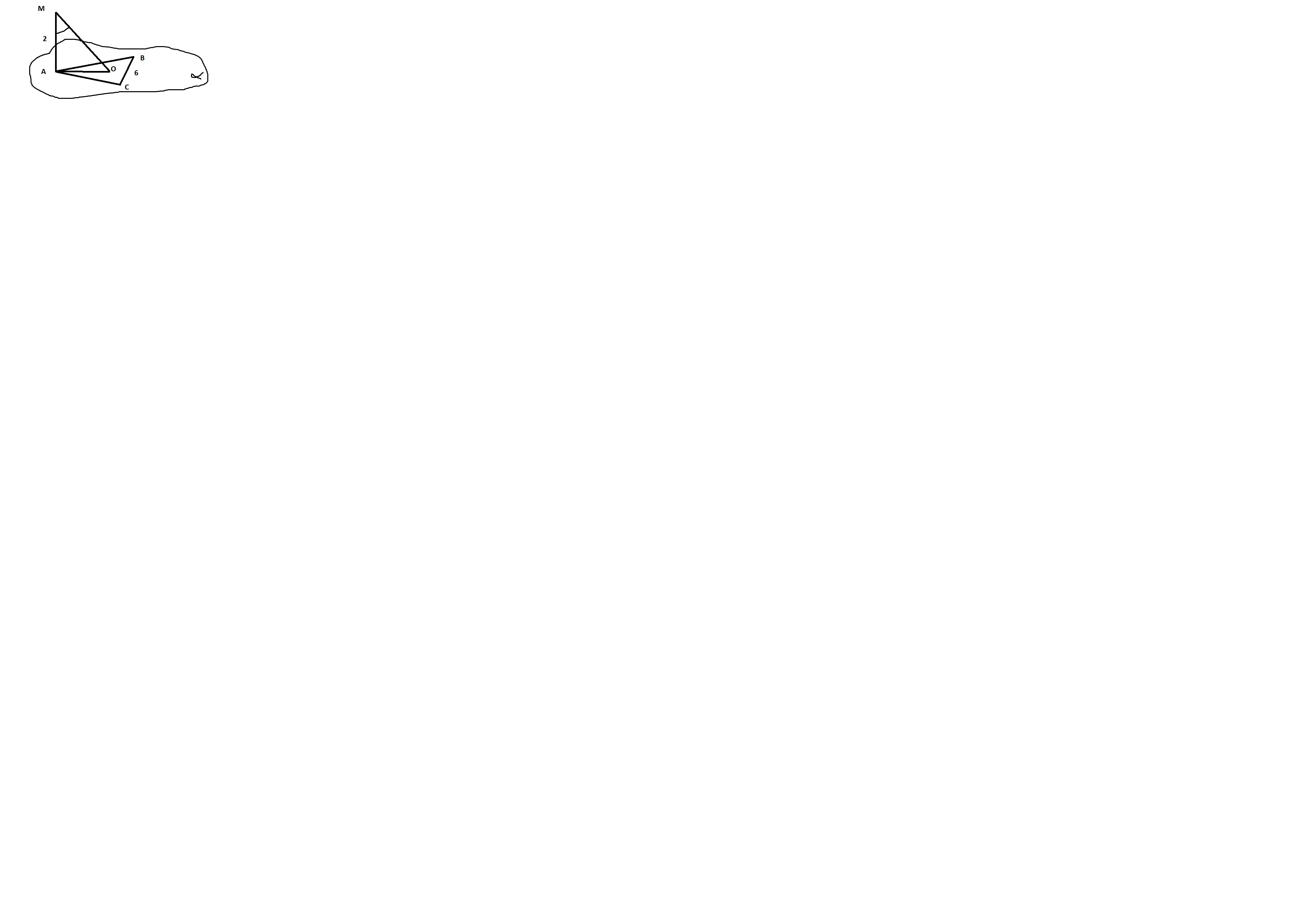
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад