Две окружности радиусов 5 и 3 имеют общий центр. Найдите длину хорды большей окружности, лежащей на касательной к меньшей окружности.
Ответы
Ответ дал:
0
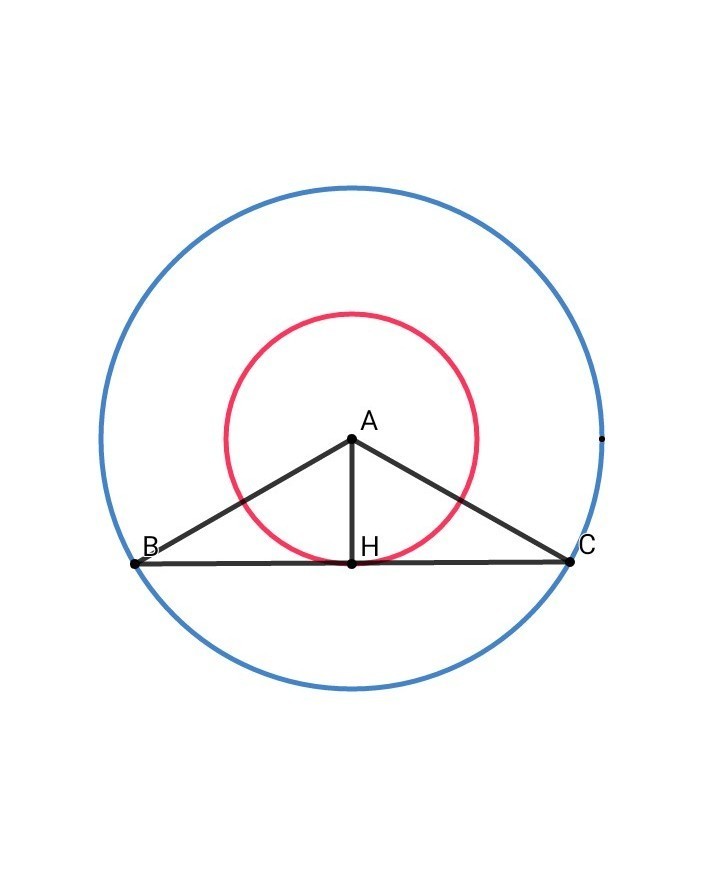
▪АВ = АС => тр. АВС - равнобедренный
АН перпендикулярен ВС по свойству радиуса окружности, проведённого в точку касания.
ВН = СН - по свойству равнобедренного треугольника
▪Рассмотрим прямоугольный тр. АНС:
По теореме Пифагора:
АС^2 = АН^2 + СН^2
СН^2 = 5^2 - 3^2 = 25 - 9 = 16
СН = 4
Значит, ВС = 2•СН = 2 • 4 = 8
☆ ОТВЕТ: 8 ☆
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад