Ответы
Ответ дал:
0
Когда основы логарифма одинаковы, мы можем сравнить подлогарифмическое выражения :
ОДз:
х+7>1
х>-6

25 > х² +14х +49
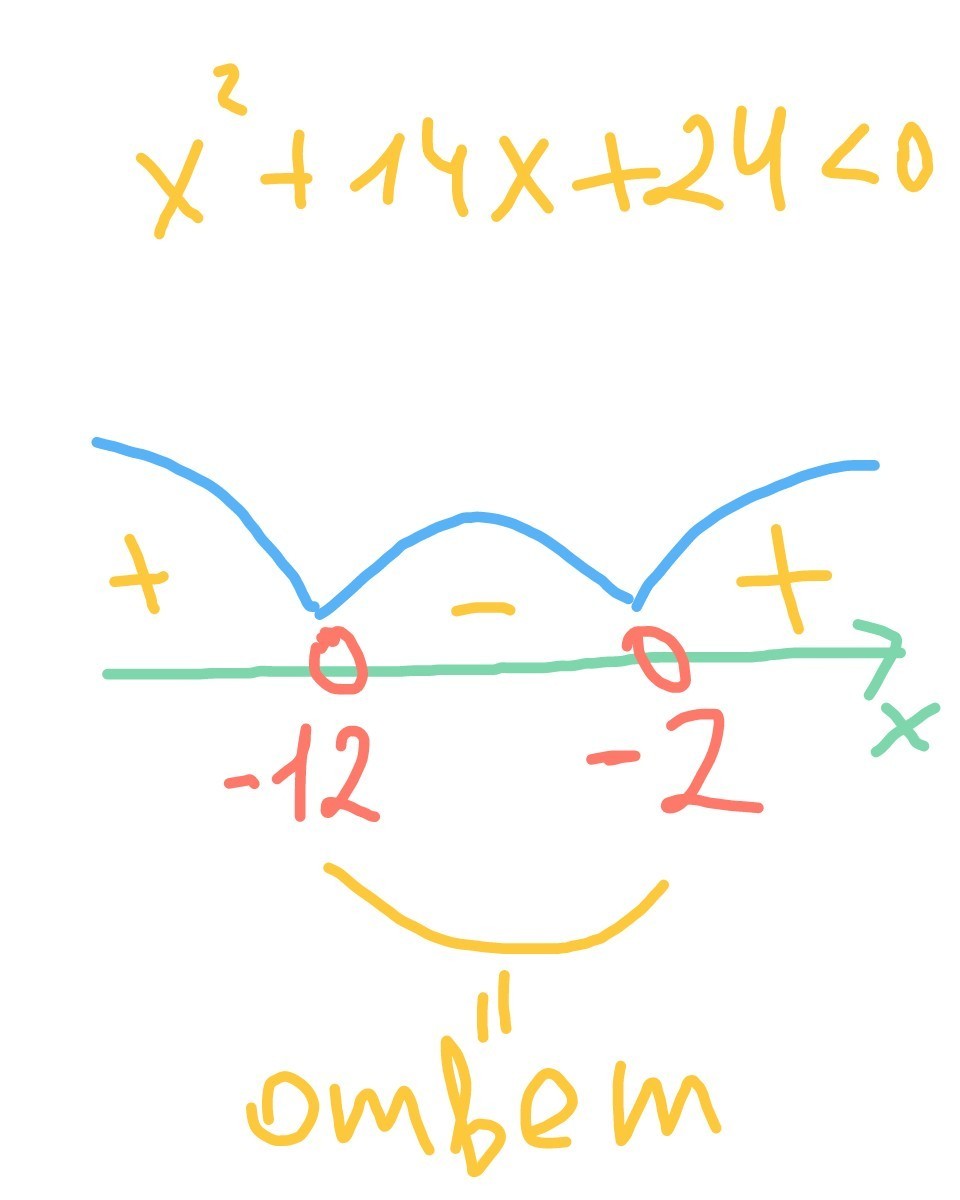
х²+14х+24<0
х²+14х+24=0
x²+12x +2x +24=0
x(x+12) +2(x+12)=0
(x+12)(x+2)=0
Корни : -12 и -2
Методом интервалов получаем:
Хє(-12;-2)
Учитывая ОДЗ
Ответ: Хэ(-6;-2)
ОДз:
х+7>1
х>-6
25 > х² +14х +49
х²+14х+24<0
х²+14х+24=0
x²+12x +2x +24=0
x(x+12) +2(x+12)=0
(x+12)(x+2)=0
Корни : -12 и -2
Методом интервалов получаем:
Хє(-12;-2)
Учитывая ОДЗ
Ответ: Хэ(-6;-2)
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад