Question

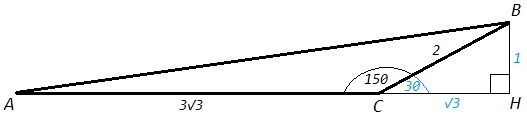
В треугольнике ABC известны стороны АС=3√3, BC=2, и угол при вершине С равен 150 градусов. Найдите длину стороны АВ.
Помогите пожалуйста!!
С рисунком!!

Answer 1

Потеор.косинусов АВ^2=AC^2+BC^2-2AC*BC*cos150=27+4-2*3V3*2(-V3 /2)=31+18=49,  AB=7

Answer 2

По теореме косинусов

AB^2= AC^2 +BC^2 -2AC*BC*cos150 =27 +4 +18 =49 <=> AB=7

Или

BH - высота на AC, ∠BCH=180-150=30

△CBH - углы 30, 60, 90, стороны относятся как 1:√3:2

BH=1, CH=√3

AH=AC+CH =3√3 +√3 =4√3

По теореме Пифагора

AB=√(AH^2 +BH^2) =√(48+1) =7

Answer 3

Здравствуйте, можете помочь с геометрией? Темы: Прямая на плоскости
Плоскость в пространстве
Прямая в пространстве
Кривые 2 порядка
Поверхность 2 порядка. Напишите мне пожалуйста в ЛС, буду вам благодарен по гроб жизни.