Question

Висота правильного трикутника дорівнює 15см,знайти радіус вписаного кола

Answer 1

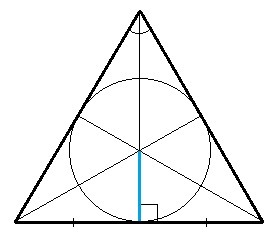
Центр окружности, вписанной в угол, лежит на биссектрисе угла. А центром окружности, вписанной в треугольник (то есть в три угла), является пересечение биссектрис углов. В равностороннем треугольнике биссектрисы являются медианами и высотами и равны между собой. Медианы треугольника точкой пересечения делятся в отношении 2:1 от вершины. Радиус вписанной окружности - перпендикуляр из центра к стороне. Таким образом, радиус вписанной окружности правильного треугольника равен 1/3 медианы.  

r=15/3=5

Answer 2

В равностороннем треугольнике со стороной a биссектрисы/медианы/высоты h=a√3/2.
Радиус вписанной окружности r= 1/3 *h =a√3/6
Радиус описанной окружности R= 2/3 *h =a√3/3