Question

СРОЧНО!!! ПОМОГИТЕ ПОЖАЛУЙСТА
Ребро основания правильной четырехугольной пирамиды равно 4√2 двугранный угол при боковом ребре равен 90°. Найдите площадь сечения, проходящего через диагональ основания перпендикулярно боковому ребру.

Answer 1

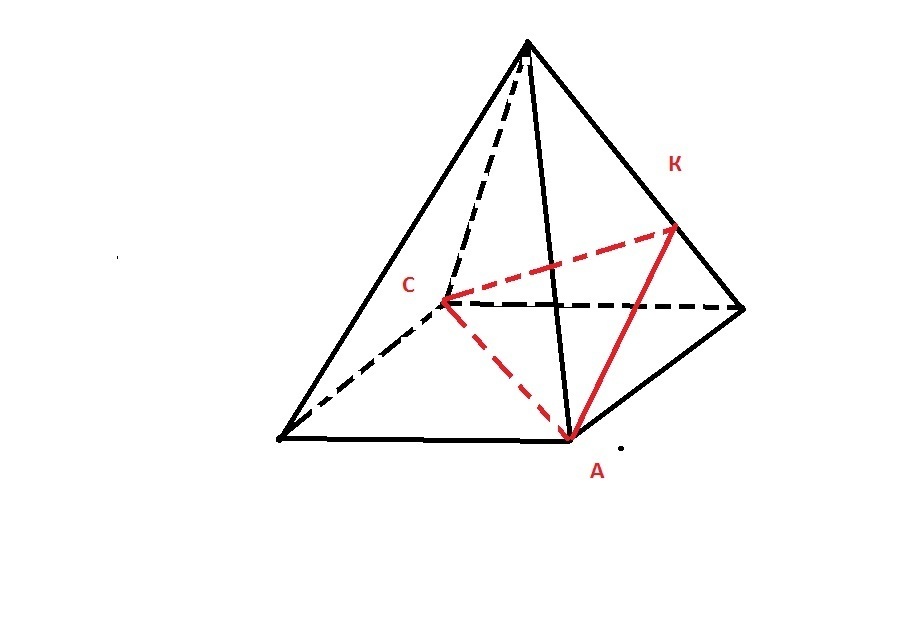
Проводим из А и из С перпендикуляры к боковому ребру. Они проходят через одну точку К, т.к. боковые грани - равные треугольники, угол АКС - линейный угол двугранного угла при боковом ребре, он по условию равен 90°. Вычисляем АС из квадрата в основании. АС=√2*а = √2*4√2=8.(а - сторона квадрата).

КС=АК=АС*sin 45° = 8*√2/2 = 4√2. S(ACK)=1/2 *CK*AK= 1/2*(4√2)²=16.

Answer 2

Зачем нужно умножать на синус45?