В сферу, радиус которой равен R, вписан куб. Вокруг этой же сферы описан куб. Найдите отношение площади полной поверхности меньшего куба к площади полной поверхности большего куба.
Ответы
Ответ дал:
0
по условию известно, что в сферу вписан куб, следовательно, диаметр сферы D = диагонали куба d
теорема о квадрате диагонали прямоугольного параллелепипеда:
d^2 = a^2+b^2+c^2
куб - прямоугольный параллелепипед, все ребра, которого равны а
d^2=3a^2
D=2R
d=2R
(2R)^2=3a^2
4R^2=3a^2
продолжение во вложении
теорема о квадрате диагонали прямоугольного параллелепипеда:
d^2 = a^2+b^2+c^2
куб - прямоугольный параллелепипед, все ребра, которого равны а
d^2=3a^2
D=2R
d=2R
(2R)^2=3a^2
4R^2=3a^2
продолжение во вложении
Приложения:
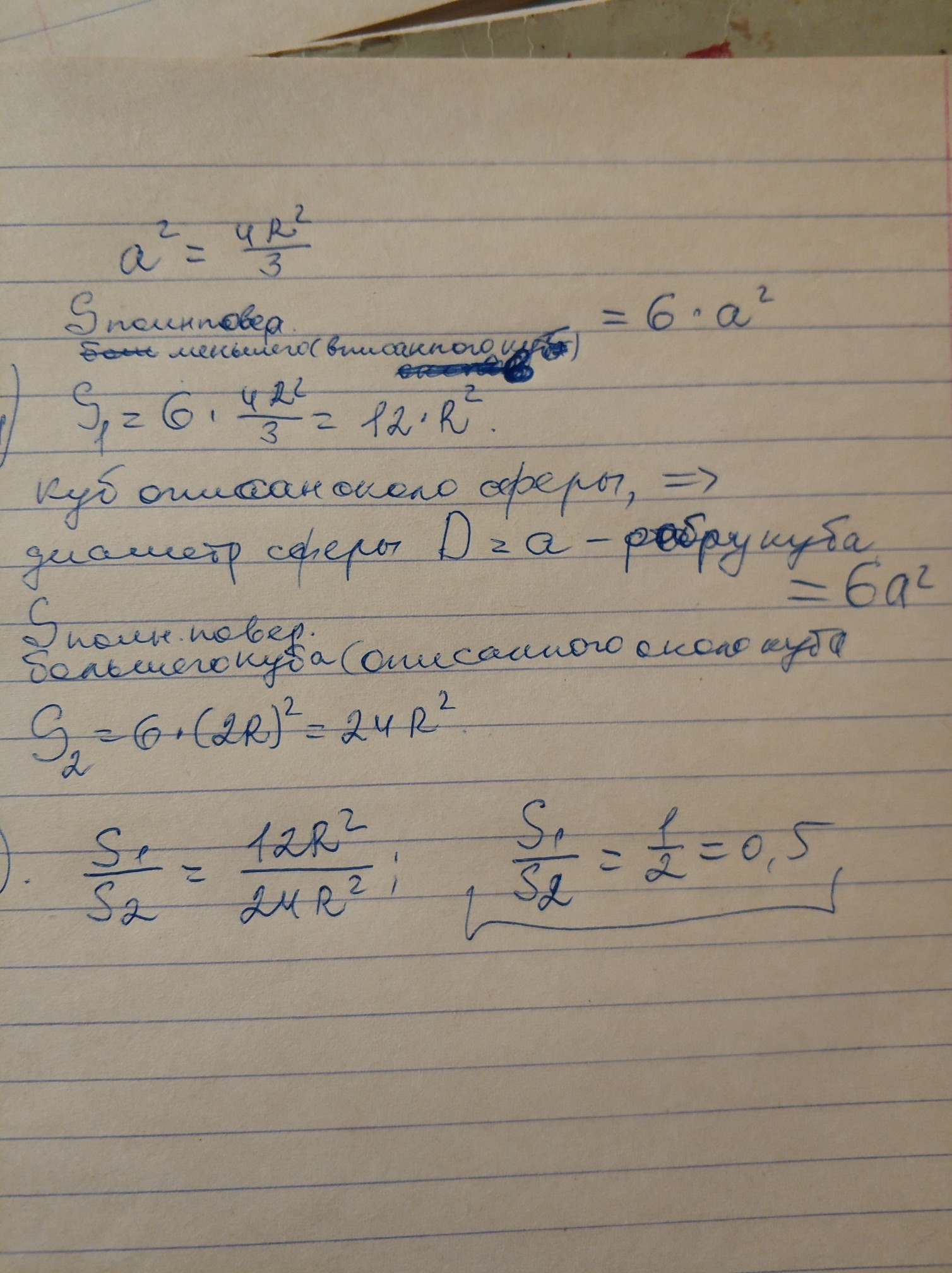
Ответ дал:
0
Заметил ошибку - 6*4=24; 24:3=8. То есть площадь 1 = 8R^2
Ответ дал:
0
спасибо, исправила. арифметика (((((??
Ответ дал:
0
неееет, не исправила. добавила не то фото
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад