ДАЮ МАКСИМУМ БАЛЛОВ
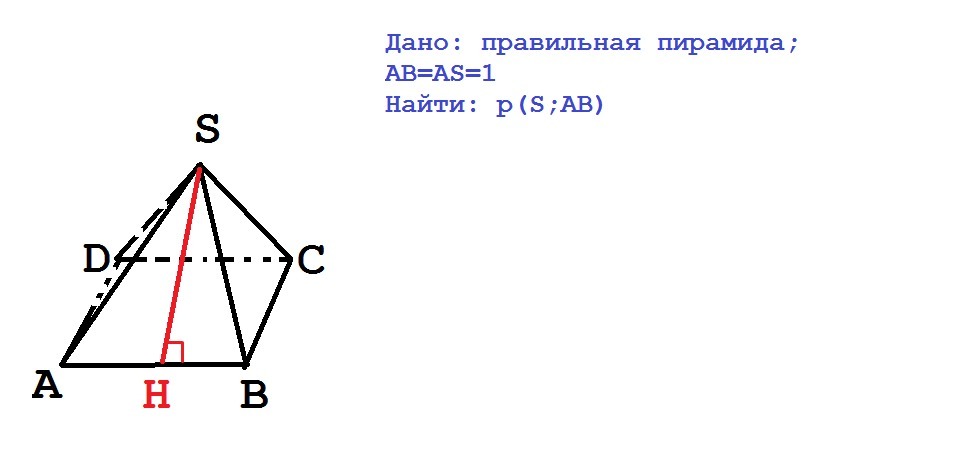
В правильной пирамиде SABCD, все ребра которой равны 1, найдите расстояние от вершины S до прямой AB.
Пожалуйста, с "дано" и чертежом!
Ответы
Ответ дал:
0
Напомню, что расстояние от точки до прямой называется перпендикуляр, опущенный из данной точки на прямую.
Рассмотрим ΔASB - равносторонний ( по условию все ребра = 1), то опустим SH ⊥ AB. По свойству равностороннего треугольника: AH = HB = 0,5.
Рассмотрим ΔSHB - прямоугольный: SB = 1; HB = 0,5. Нужно найти катет SH, то по т.Пифагора: SH = √(SB^2 - HB^2) = √3/√4 = √3/2
Ответ: √3/2
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад