Здравствуйте! Помогите, пожалуйста, решить логарифммческое неравенство. Желательно с объяснениями и полным решением.
Спасибо!
Приложения:
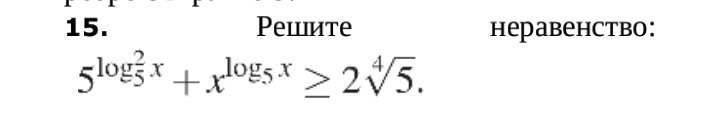
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад