Question

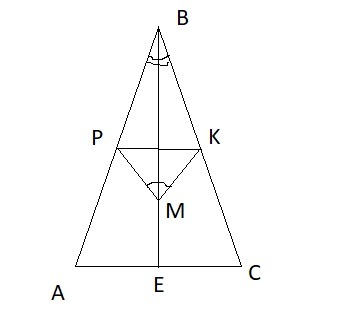
Дано: ABC- треугольник
АB=BC
BE - медиана
М лежит на стороне BE
P лежит на стороне AB
К лежит на стороне BC
Угол BMP = углу BMK
Док-ть:
а)угол BPM= углу BKM
б)Прямая PK перпендик. BM

Answer 1

Ответ:

Пошаговое объяснение:

а) Медиана проведенная к основанию равнобедренного треугольника является одновременно его биссектрисой, следовательно ∠PBM = ∠KBM. По условию ∠BMP = ∠BMK.

Следовательно ΔBPM = ΔBKM (у них общая сторона BM. к которой прилегают два равных угла). Из равенства этих треугольников и следует, что ∠BPM= ∠BKM.

б) В пункте а) доказано, что ΔBPM = ΔBKM, откуда следует, что BP = BK. Следовательно PK || AC.

А AC ⊥ BE (т.к. медиана проведенная к основанию равнобедренного треугольника является одновременно его высотой). Значит и PK ⊥ BE ⇒ PK ⊥ BM

Answer 2

Спасибо