Question

Допоможіть зробити завдання по математиці за 8 клас!! Відам усі балли!

Answer 1

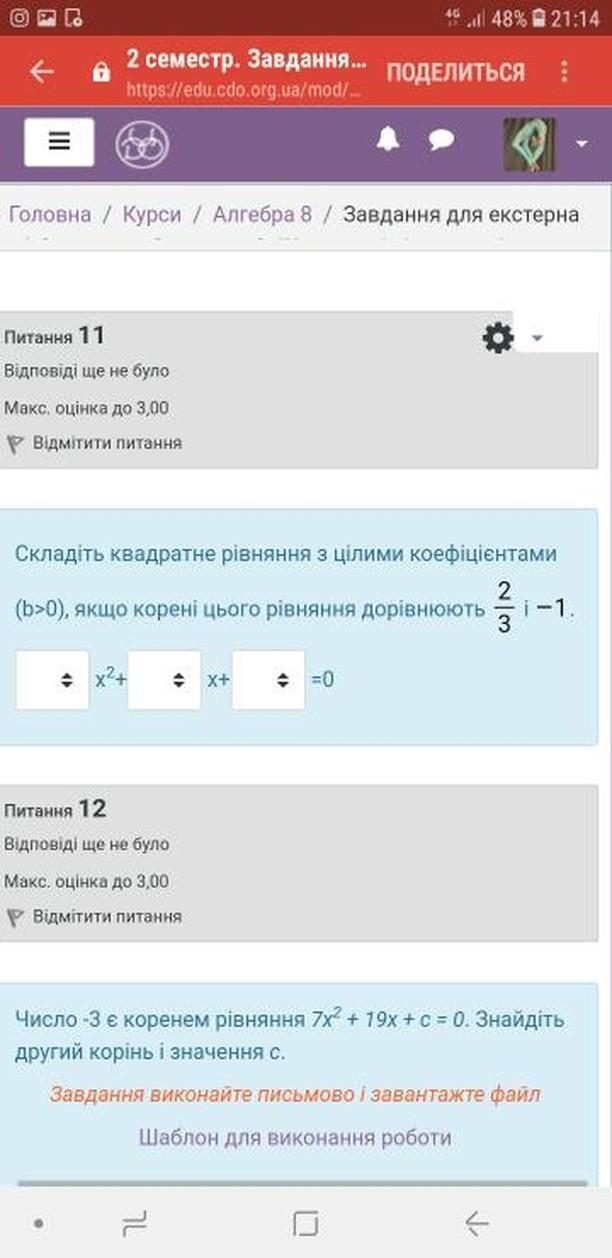
Питання 11.

Якщо корені квадратного рівняння відомі $x_1=frac{2}{3},x_2=-1,$ то саме рівняння можна записати у вигляді:

$left(x-frac{2}{3}right)(x+1)=0$

і, розкривши дужки та помноживши все рівняння на 3, отримуємо

$3x^2+x-2=0$

Також можна скористатись теоремою Вієта:

$x^2-left(frac{2}{3}+(-1)right)x+frac{2}{3}cdot(-1)=0$

$3x^2+x-2=0$.

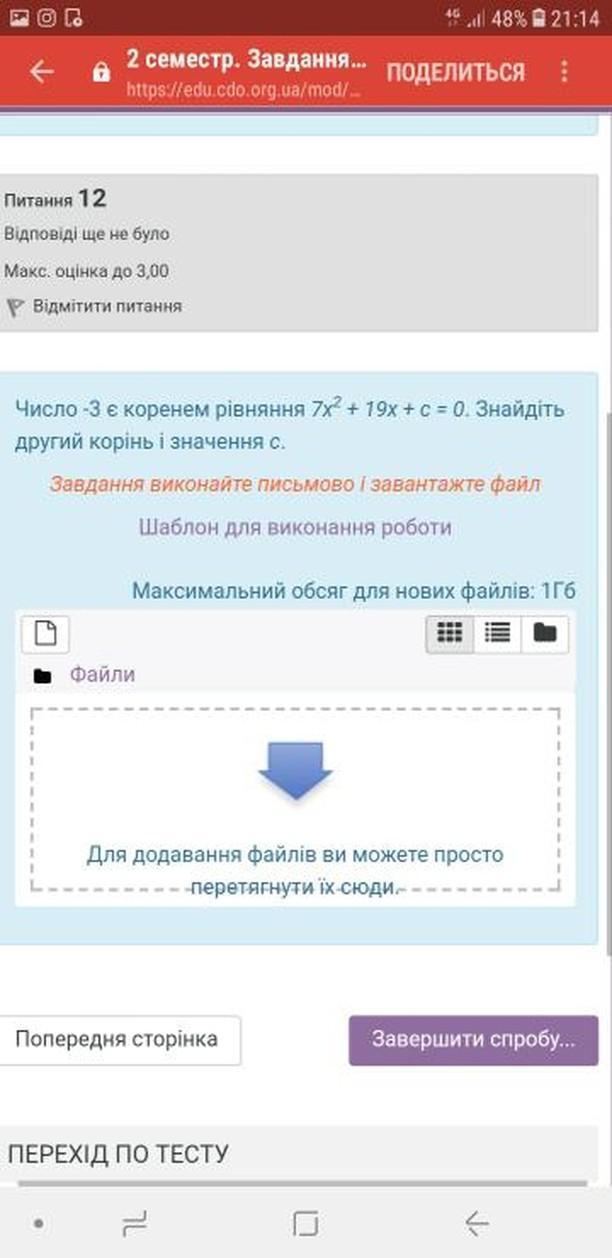
Питання 12.

З теореми Вієтта другий корінь рівняння буде дорівнювати:

$x_2=-frac{19}{7}-x_1=-frac{19}{7}-(-3)=frac{2}{7}$

Тоді значення с буде:

$c=7cdotfrac{2}{7}cdot(-3)=-6$

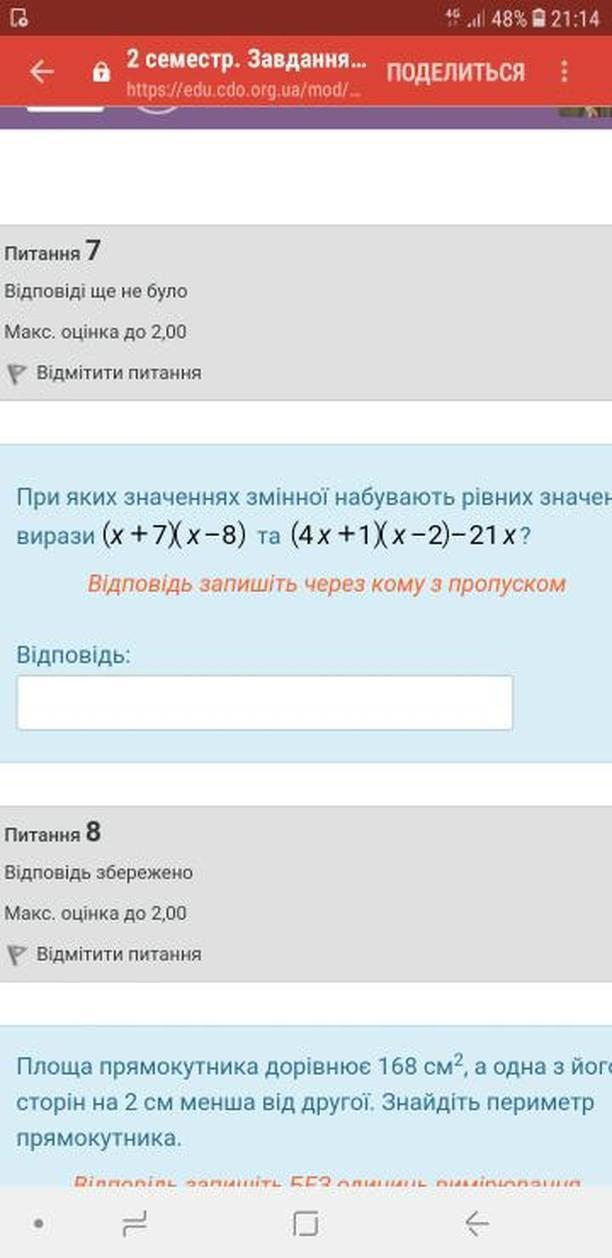
Питання 7.

Порібно розв'язати рівняння:

$(x+7)(x-8)=(4x+1)(x-2)-21x;\x^2+7x-8x-56=4x^2+x-8x-2-21x;\3x^2-27x+54=0;\x^2-9x+18=0;\x_1=3;,x_2=6.$

(корені знайдені за теоремою Вієта: їх добуток 18, а сума 9)

Питання 8.

Якщо позначити меншу сторону прямокутника за x, то за умовою його більша сторона буде дорівнювати x+2 і маємо рівняння:

$x(x+2)=168;\x^2+2x-168=0;\D=b^2-4ac=4-4cdot(-168)=4+672=676=26^2;\x_1=frac{-b+sqrt{D}}{2a}=frac{-2+26}{2}=12;\x_2=frac{-b-sqrt{D}}{2a}=frac{-2-26}{2}=-14<0.$

Другий знайдений корінь рівняння не може задовольняти умову задачі, тому сторони прямокутника дорівнюють 12 см і 12+2=14 см, а периметр дорівнює:

$P=(12+14)cdot2=52$ сантиметра.