Question

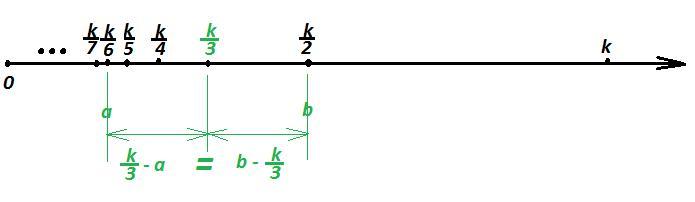
Назовём натуральное число k олимпиадным, если у него есть два раз- личных натуральных делителя a и b на одинаковом расстоянии от числа k/3 (то есть |a−k/3| = |b−k/3|). Сколько существует олимпиадных чисел, не превосходящих 2018?

Answer 1

Подставим в равенство

$|a-frac{k}{3}|=|b-frac{k}{3}|$

выражение $k=acdot b$

Тогда получим:

$acdot|3-b|=bcdot|3-a|,$

и, поскольку a и b разные числа, то

$acdot(b-3)=bcdot(3-a);\2ab-3a-3b=0;\b=-frac{3a}{2a-3};\a=2,b=6;,,a=3,b=3;\k=12,,k=9$

То есть, существует только два таких числа: 9 и 12

Answer 2

все же 9 тоже не подходит так как a и b - должны быть разными.

Answer 3

Расположим делители числа  k  в порядке возрастания (естественно, если такие делители существуют).

$boldsymbol{1;~2;~3;~4;~5;...~dfrac k5;~dfrac k4;~dfrac k3;~dfrac k2;~k}$

Пусть a < b.

Так как различные натуральные делители a и b расположены на одинаковом расстоянии от числа k/3,  то расположены они по разные стороны от числа k/3

     $a<dfrac k3<b$

На числовой оси правее числа k/3 ( то есть больше числа k/3) расположены только два делителя :  само число k  и  k/2.

b = k   не подходит по условию, так как делитель a тогда отрицательный

$a = dfrac k3-bigg(b-dfrac k3bigg)=dfrac k3-b+dfrac k3=dfrac {2k}3-k=-dfrac k3$

Остаётся единственный вариант  $boldsymbol{b=dfrac k2}$

$bigg|b-dfrac k3bigg|=b-dfrac k3=dfrac k2-dfrac k3=dfrac k6\\bigg|a-dfrac k3bigg|=dfrac k3-a=dfrac k6\\a=dfrac k3-dfrac k6;~~Rightarrow~~boldsymbol{a=dfrac k6}$

Так как у делителей  $boldsymbol{b=dfrac k2;~a=dfrac k6}$  общий знаменатель равен 6, то олимпиадными будут все числа, кратные 6. Тогда олимпиадных чисел, не превосходящих 2018:

2018 : 6 = 336,(3)   -    336 чисел

Проверка :

k=6;     b=3;   a=1;    |1-2|=|3-2| =1

k=12;   b=6;   a=2;   |2-4|=|6-4| =2

k=18;   b=9;   a=3;   |3-6|=|9-6| =3  ...

$k=2016;~~~dfrac k3=672;~~~b=dfrac k2=1008;~~~a=dfrac k6=336\bigg|a-dfrac k3bigg|=Big|336-672Big|=336=bigg|b-dfrac k3bigg|=Big|1008-672Big|=336$

Ответ : 336 чисел