Question

В треугольнике АВС точка К принадлежит АВ и АК:КВ=4:7. Через вершину В
проведена прямая, параллельная отрезку СК, пересекающая продолжение
стороны АС в точке D. Найти BF:FC, если точка E – середина BD, а прямая AE
пересекает сторону BC в точке F.
Ответ дайте в виде целого числа или десятичной дроби.

Answer 1

В треугольнике АВС точка К принадлежит АВ и АК:КВ=4:7. Через вершину В

проведена прямая, параллельная отрезку СК, пересекающая продолжение

стороны АС в точке D. Найти BF:FC, если точка E – середина BD, а прямая

Answer 2

напиши решение, ничего не понятно

Answer 3

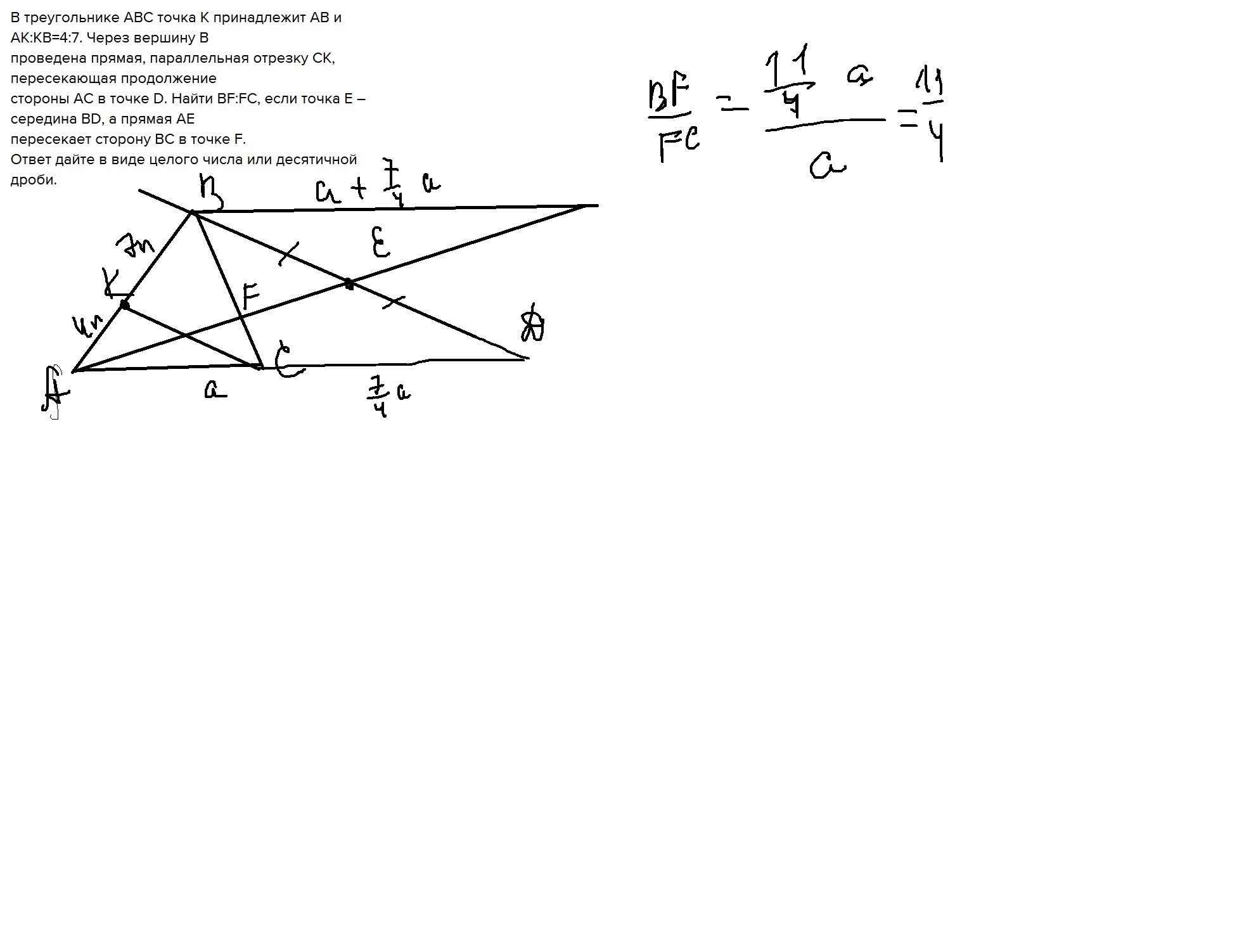
Обозначим АС=а. ∆АКС∼∆АВД , значит АК/АВ=АС/АД, т.е. 4/11=а/АД⇒ АД=11/4 а. Проведем через точку В прямую параллельную АД, пусть М-точка пересечения ее с прямой АЕ. Тогда ∆ВЕМ=∆ДЕА и АД=ВМ=11/4 а. ∆АFC∾∆МFВ, значит ВF/FC=,ВМ/АС т.е ВF/FC=11/ а /а=11/4.

Answer 4

Смотри, могут быть и ошибки.