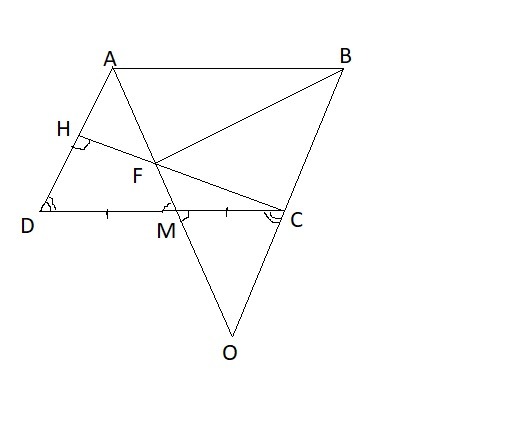
Вершину тупого угла А параллелограмма ABCD соединили с точкой M - серединой его стороны CD. Высота CH параллелограмма , опущенная на сторону AD, пересекает отрезок AM в точке F. Найдите BF, если AF=4 и FM=1
Ответы
Ответ дал:
0
Продолжим отрезок AM до пересечения с продолжением стороны BC в точке O.
DM = MC (по условию)
∠AMD = ∠OMC (как вертикальные)
∠ADM = ∠MCO (как накрест лежащие) ⇒
ΔAMD = ΔMCO (по стороне и двум прилежащим углам)
Тогда MO = AM и OC = AD = BC
Следовательно в ΔFBO FC является медианой и одновременно высотой (CH ⊥ AD , AD ║ BC ⇒ CH ⊥ BO ⇒ FC ⊥ BO)
Отсюда ΔFBO равнобедренный и BF = FO = FM + MO = FM + AM = FM + AF + FM = AF + 2*FM = 6
Приложения:
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад