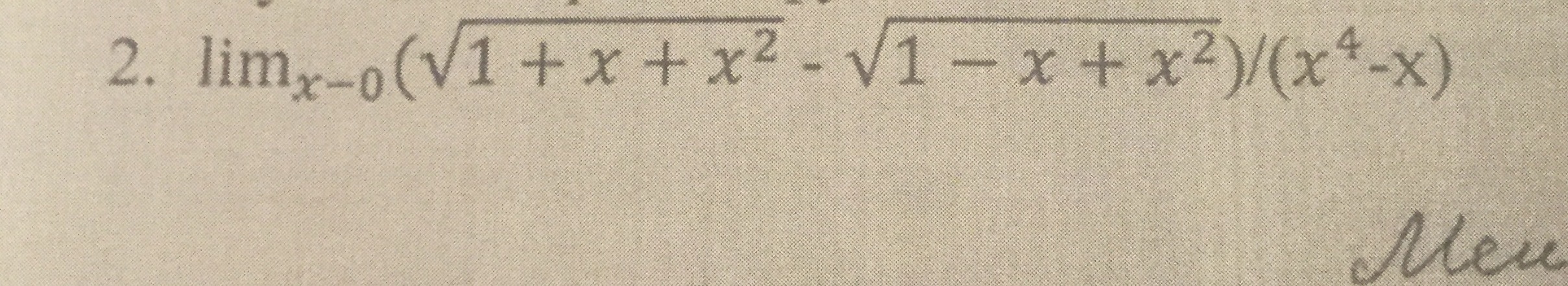Ответы
Ответ дал:
0
Домножим и числитель, и знаменатель на выражение, сопряженное числителю:
Oтвет: - 1
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад