Question

одна из диагоналей параллелограмма , длина которой 80 см, образует с его сторонами углы 10градусов и 20 градусоа. найтм площадь параллелограмма

Answer 1

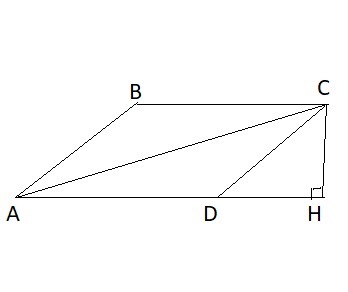
AC=80;∠CAD=10°;∠CAB=20°;

В параллелограмме ABCD опустим высоту CH.

Из прямоугольного ΔACH

$CH=AC*sin(widehat{CAD})=80sin10dot{}$

$AH=AC*cos(widehat{CAD})=80cos10dot{}$

∠ADC = 180° - ∠BAD = 180° - (∠CAD + ∠CBA) = 150°

∠CDH = 180° - ∠ADC = 30°

Из прямоугольного ΔCDH

$DH=frac{CH}{tg(widehat{CDH})}=frac{80sin10dot{}}{tg(30dot{})}=80sqrt{3}sin10dot{}$

$AD=AH-DH=80cos10dot{}-80sqrt{3}sin10dot{}=160*(frac{1}{2}cos10dot{}-frac{sqrt{3}}{2}sin10dot{})=160*cos{70dot{}}$

Найдем площадь параллелограмма:

$S=AD*CH=160*cos{70dot{}}*80sin10dot{}=12800*cos{70dot{}}*sin10dot{}$