требуется выполнить действия вычитания и деления комплексных чисел z1, z2.
z1 = (-5+i) , z2 = (3+2i).
- - -
меня смущает одно , полоска сверху - это отрицание? если да, то когда применять отрицание, после решения или перед ним?
Приложения:
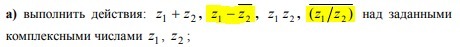
Ответы
Ответ дал:
0
Ответ дал:
0
окончательный ответ 1 - i?
Ответ дал:
0
поправочка , -1 - i?
Ответ дал:
0
как я могу с вами связаться? обмен сообщениями недоступен тут говориться.
Ответ дал:
0
я исправила условие и решение
Ответ дал:
0
благодарю.
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад
10 лет назад