Question

Найдите площадь треугольника ABC

Answer 1

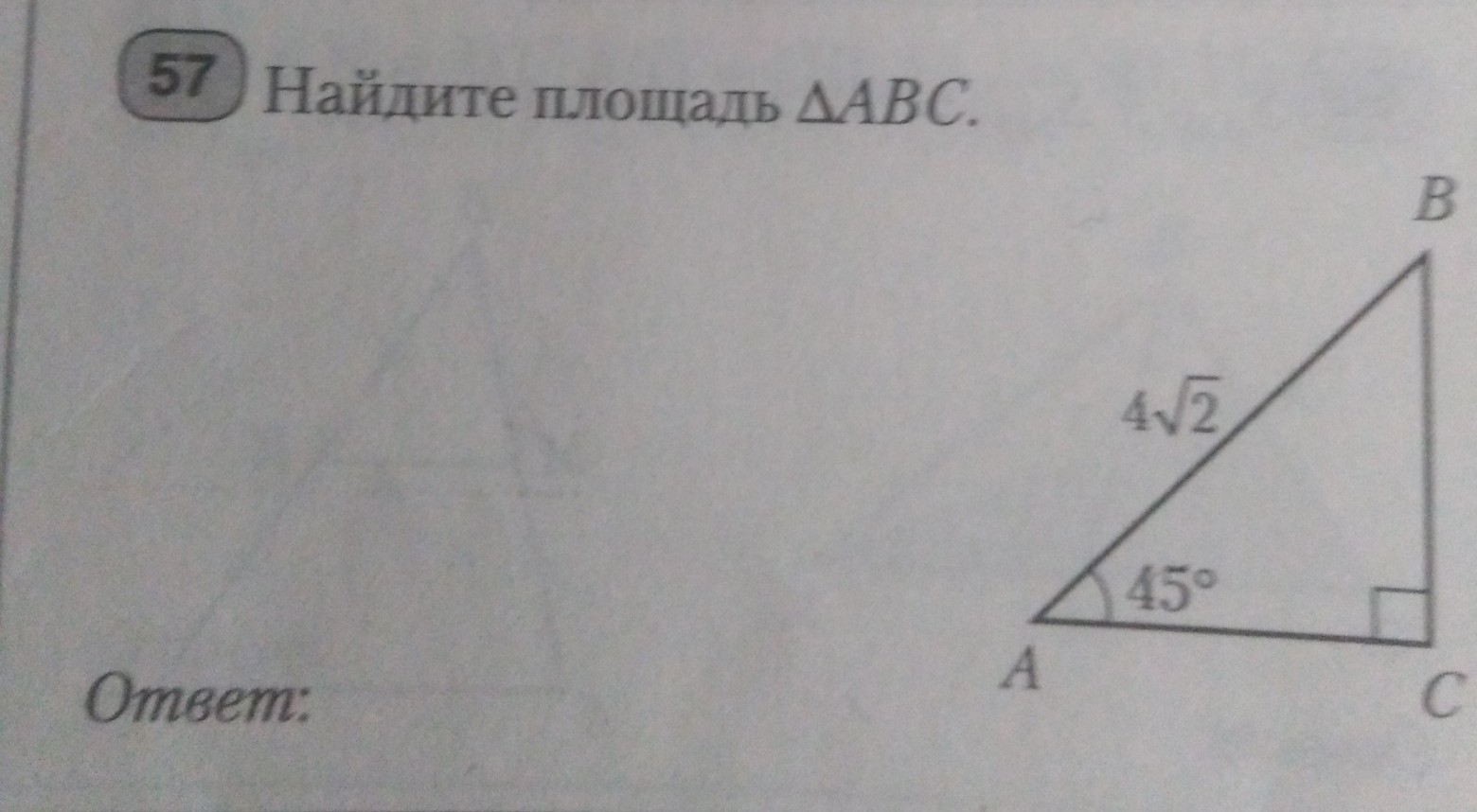
∠B = 90°-45° = 45°.

В равнобедренном треугольнике углы при основании равны.

Значит ΔBCA - прямоугольный равнобедренный прямоугольник,

где AB - основание, а BC = AC;

AB² = 2AC²

32 = 2AC²

AC² = 16

AC = 4 ( см)

Площадь прямоугольного треугольника: S = ab/2 , где a,b - катеты прямоугольного треугольника.

Отсюда S = 4*4/2 = 8 см²

Answer 2

Здравствуйте!

∠А=45°С ⇒ ∠В=90°-45°=45° ⇒ ΔАВС - равнобедренный, АС=СВ.

Найдем АС и ВС по Теореме Пифагора: пусть х см - АС=ВС.

$x^{2} +x^{2} =(4sqrt{2} )^{2} \2x^{2} =32\x=4$

АС=ВС=4 см

SΔabc=$0,5*4*4=8 cm^{2}$

Ответ: 8 см²

Удачи в учебе!

Answer 3

Ошибка в записи решения уравнения. х^2 + х^2 = 16*2; 2*х^2 = 32. Исправьте, пожалуйста, решение.

Answer 4

Спасибо, исправила.