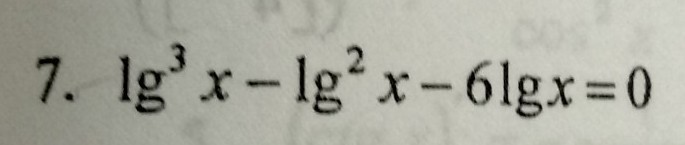Question

ПАМАГИТИ ПОЖУЙЛИСТА СРОЧНО НИКТО НЕ МОЖЕТ РЕШИТЬ

Answer 1

Пусть lg(x)=t, тогда мы получаем кубическое уравнение t³-t²-6*t=0, или t*(t²-t-6)=0. Отсюда либо t1=0, либо t²-t-6=0. Второе уравнение имеет решения t2=3 и t3=-2. Тогда x1=10^t1=10^0=1, x2=10^t2=10³=1000, x2=10^t3=10⁻²=0,01. Ответ: x1=1, x2=1000, x3=0,01.  

Answer 2

Хотя сам вижу. Сейчас исправлю решение.

Answer 3

Там не t^2-t-61=0, а t^2-t-6=0. Это уравнение имеет корни t2=3 и t3=-2, так что x2=10^3=1000 и x3=10^(-2)=0,01. Ответ: 0, 1000, 0,01.

Answer 4

Букву l перепутал с цифрой 1, отсюда и ошибка.

Answer 5

спс

Answer 6

Решение изменено.