Question

Помогите
Преобразовать ур-е кривой второго порядка к каноническому виду, построить её и найти параметры, определяющие данную линию.

2x²+3y²-2x+6y=0

Answer 1

Ответ:

Это эллипс

$frac{(x-0,5)^2}{1,75}+frac{(y+1)^2}{1,1(6)}=1$

Пошаговое объяснение:

2x²-2x+3y²+6y=0

2(x²-x+0,25-0,25)+3(y²+2y+1-1)=0

2(x-0,5)²-0,5+3(y+1)²-3=0

2(x-0,5)²+3(y+1)²=3,5

$frac{(x-0,5)^2}{frac{3,5}{2} } +frac{(y+1)^2}{frac{3,5}{3} }=1$

$frac{(x-0,5)^2}{1,75}+frac{(y+1)^2}{1,1(6)}=1$

Это эллипс

Его большая полуось равна  $a=sqrt{1,75}approx 1,323,$

малая полуось равна  $b=sqrt{1,1(6)}approx 1,08$.

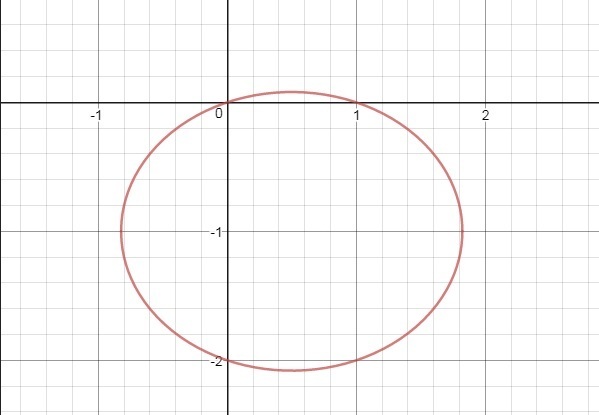
Центр эллипса в точке (0,5; -1) .

Эксцентриситет e равен

$c=sqrt{a^2-b^2}=sqrt{frac{3,5}{2}-frac{3,5}{3} }=sqrt{frac{3,5}{6}}=sqrt{0,58(3)}approx0,763763$ - это расстояние от центра эллипса до фокуса.

$e=frac{c}{a}approxfrac{0,763763}{1,323} approx0,5773$ - это эксцентриситет эллипса.

Приблизительные координаты фокусов

F₁(≈0,5-0,763763; -1) и F₂(≈0,5+0,763763; -1)

F₁(≈ -0,263763; -1) и F₂(≈1,263763; -1)

Координаты вершин эллипса

Левая вершина равна (≈0,5-1,323; -1) или (≈  -0,823; -1)

Правая вершина (≈0,5+1,323; -1) или (≈1,823; -1)

Верхняя вершина равна (0,5; -1+1,08) или (0,5; ≈0,08)

Нижняя вершина равна (0,5; -1-1,08) или (0,5; ≈ -2,08)

Директрисы эллипса

Нужно найти разность между правой вершиной и правым фокусом - это расстояние будет равно

1,823-1,263763=0,558237

Это расстояние - расстояние между соответствующими вершинами и директрисами.

Директрисы параллельны оси ординат.

Левая директриса будет равна разности между левой вершиной и 0,558237.

х≈ -0,823-0,559237  или х≈ -1,382237

Правая директриса будет равна сумме между правой вершиной и 0,558237.

х≈ 1,823+0,559237  или х≈ 2,382237