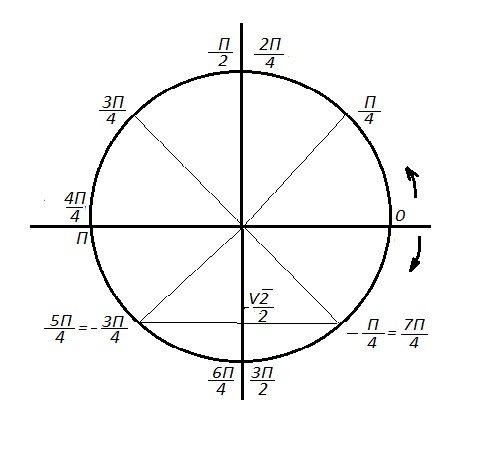
Помогите пожалуйста. Вообще понять не могу, вроде область определения у синуса от п/2 до -п/2 и вообще както работает?
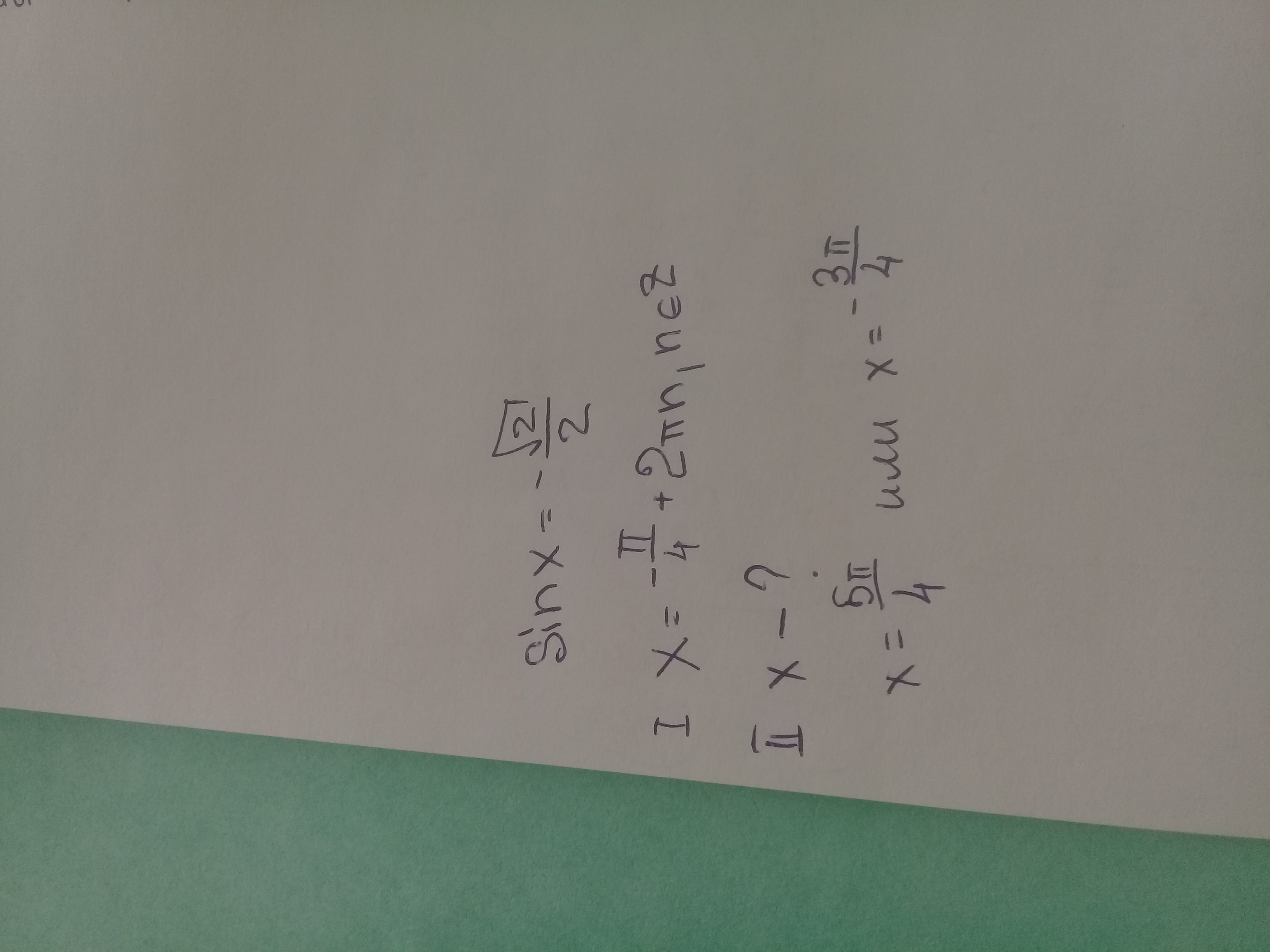
Ответы
Полученная запись решения объединяет два ответа, которые можно записать как совокупность двух решений:
Если двигаться по единичной окружности по часовой стрелке (в отрицательном направлении) , то пройдём 3 раза по , в ответе пишем угол
. Если двигаться против часовой стрелки (в положительном направлении) , то пройдём 5 раз по
, тогда пишем угол
. Эти углы соответствуют одной и той же точке на единичной окружности. Поэтому оба ответа правильны. Также можно и угол
записать как
. Выбираем те обозначения, которые нравятся.
2) Область определения функции у=sinx - это все действительные числа, то есть . На промежутке
функция y=sinx монотонно возрастает , поэтому на этом промежутке можно определить обратную функцию для y=sinx - это y=arcsinx .