Question

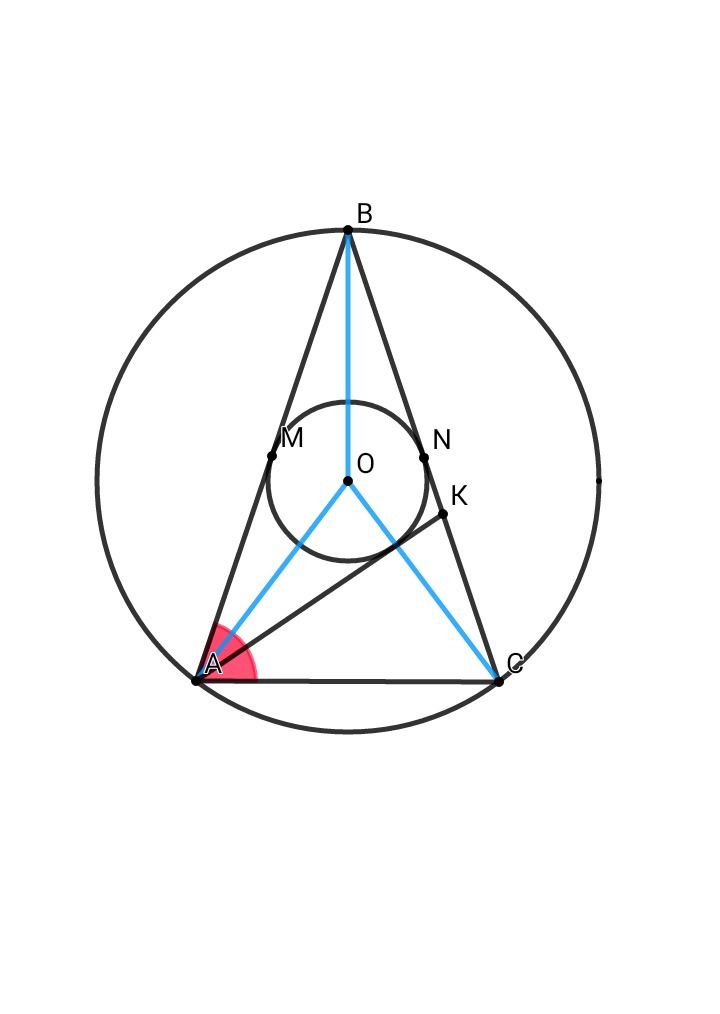
В треугольнике АВС проведены биссектрисы А К. Центр окружности, вписанного в треугольник АК В, совпадает с центром окружности, описанной около треугольника АВС. Найдите углы треугольника АВС. ДАЮ МНОГО БАЛЛОВ!!!!!!!

Answer 1

Центром вписанной окружности является точка пересечения биссектрис  ⇒  ∠КВО = ∠АВО , ∠ВАО = ∠КАО

АО = ВО = СО - по условию ⇒  ΔАОВ , ΔВОС , ΔАОС - равнобедренные.

Углы при основании равнобедренного треугольника равны ⇒  ∠АВО = ∠ВАО , ∠СВО = ∠ОСВ . Но ∠СВО = ∠АВО

Значит, ∠АВО = ∠ВАО = ∠СВО = ∠ОСВ = ∠КАО = α

АК - биссектриса ∠А - по условию  ⇒  ∠ВАК = ∠САК = ∠ВАО + ∠КАО = α + α = 2α

ΔАОС - равнобедренный  ⇒  ∠ОАС = ∠АСО = ∠ОАК + ∠САК = α + 2α = 3α

Рассмотрим ΔАВС: ∠А + ∠В + ∠С = 180°

2α + 4α + 4α = 180°

10α = 180°  ⇒  α = 18°

Значит, ∠В = 2α = 2•18° = 36° , ∠А = ∠С = 4α = 4•18° = 72°

ОТВЕТ: 36°, 72°, 72°