Question

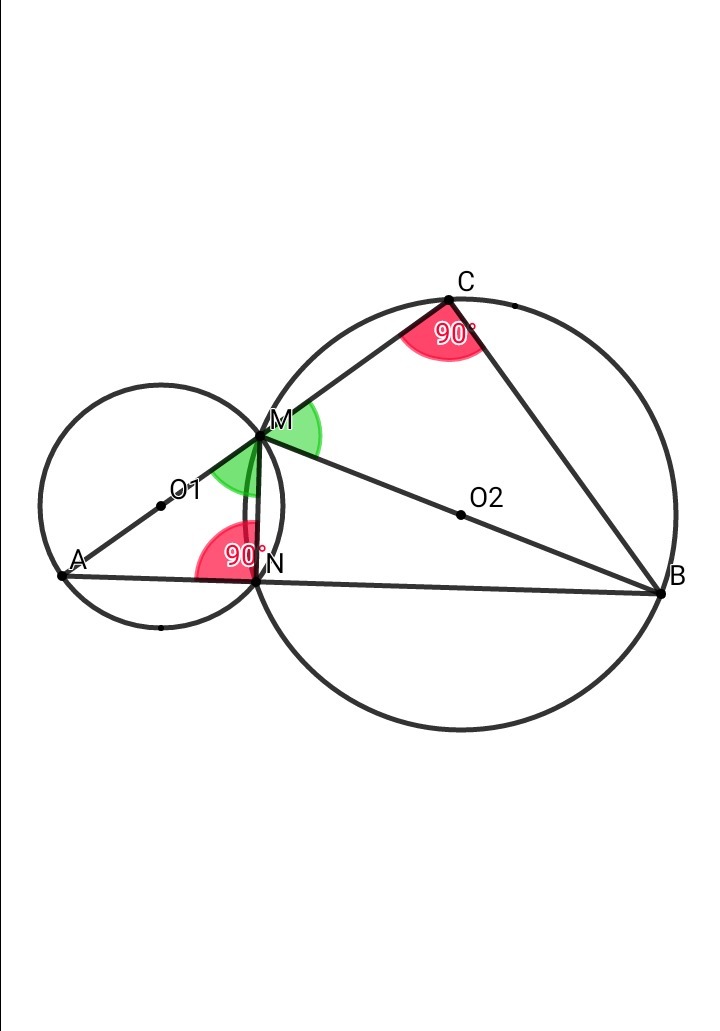
Две окружности с центрами O1 и O2 пересекаются в точках M и N, причём точки O1 и O2 лежат по разные стороны от прямой MN. Продолжение диаметра AM первой окружности и хорды AN этой же окружности пересекают вторую окружность в точках C и B соответственно. Найдите MC, если угол CMB равен углу NMA, а радиус второй окружности в 2,5 раза больше радиуса первой и MN = 2.

Answer 1

AM - диаметр первой окружности, по условию  ⇒  ∠ANM = 90° ,  AB⊥MN

∠MNB = 90°  ⇒  MB - диаметр второй окружности ⇒ ∠МСВ = 90°

В прямоугольных треугольниках ANM и MCB  ∠NMA = ∠CMB - по условию:

cos∠NMA = cos∠CMB  ⇒  MN/AM = MC/MB

MC = MN•MB/AM = MN•R₂/R₁ = 2 • 2,5 = 5

ОТВЕТ: 5