Ответы
Ответ дал:
0
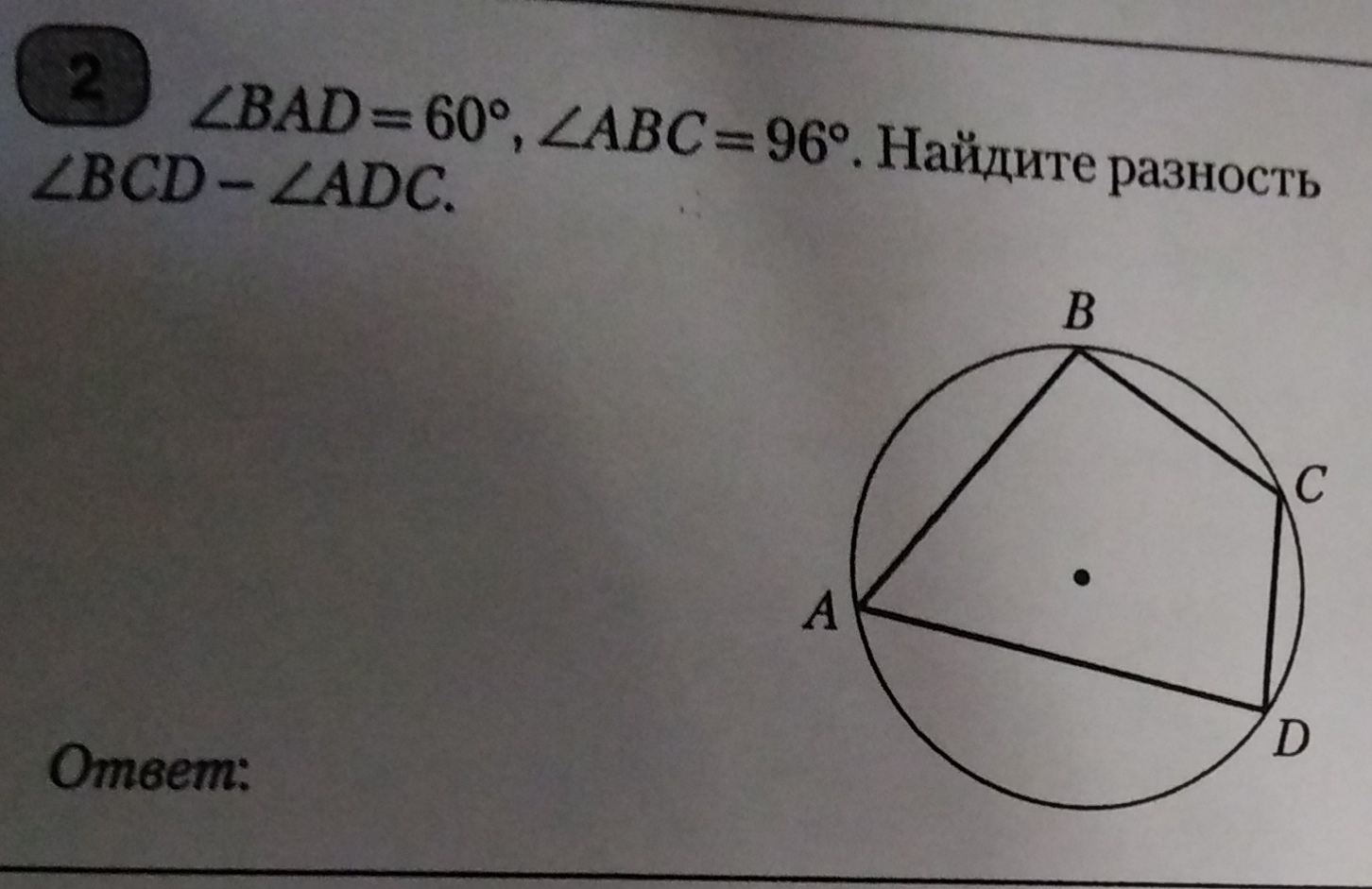
Четырехугольник можно вписать в окружность, если сумма его противолежащих углoв рaвна 180º.
Тогда ∠ADC=180°-∠ABC=180°-96=84°
∠BCD=180°-∠BAD=180°-60°=120°⇒
∠BCD-∠ADC=120°-84°=36°.
Ответ дал:
0
1. т.к окружность описана около данного четырёхугольника, то сумма противолежащих углов равна 180 градусам.
=> ∠ BDC + ∠ BAD = 180°
∠ BDC=180°- 96° = 84 °
2. Аналогично другой угол
∠ ADC=180° - 96° = 84°
3. Находим разность двух углов
∠ BCD - ∠ ACD = 120° - 84° =36°.
Ответ: 36 градусов
=> ∠ BDC + ∠ BAD = 180°
∠ BDC=180°- 96° = 84 °
2. Аналогично другой угол
∠ ADC=180° - 96° = 84°
3. Находим разность двух углов
∠ BCD - ∠ ACD = 120° - 84° =36°.
Ответ: 36 градусов
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад