Помогите пожалуйста
найдите площадь боковой поверхности и объем правильной четырёхугольной пирамиды, если сторона основания равна a, диагональное сечение равновелико основанию.
Ответы
Ответ дал:
0
В основании квадрат, его S=a^2
Диагональное сечение-это равнобедренный треугольник с основанием , травным диагонали квадрата-основания
Основание треугольника a√2, его S=a√2*h/2=ah/√2
Тогда если площадь диагонального сечения равна площади основания
ah/√2=a^2
тогда h=a^2*√2/a=a/√2
V=S(осн)*h/3=a^2*a/(3√2)=a^3/(3√2)
Боковая поверхность состоит из 4 одинаковых равнобедренных треугольника с основанием а и высотой b, которую я сейчас посчитаю...
b=a√3/2
S(бок)=4*a*a√3/4=a^2√3
Приложения:
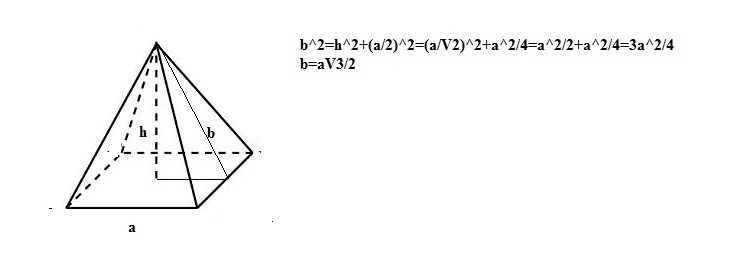
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад