Question

Помогите пожалуйста с алгеброй.

Answer 1

$1); ; sinx, cos6x-sin3x, cos4x=\\=frac{1}{2}(sin7x+sin(-5x))-frac{1}{2}(sin7x+sin(-x))= frac{1}{2}(sinx-sin5x)=\\=sinfrac{x-5x}{2}cdot cosfrac{x+5x}{2}=-sin2xcdot cos3x$

$2); ; sina, sin(beta -a)+sin^2(frac{beta }{2}-a)=sin^2frac{beta }{2}; ; Rightarrow \\sina, sin(beta -a)=sin^2frac{beta }{2}-sin^2(frac{beta }{2}-a); ;\\\sin^2frac{beta }{2}-sin^2(frac{beta }{2}-a)=(sinfrac{beta }{2}-sin(frac{beta }{2}-a))cdot (sinfrac{beta }{2}+sin(frac{beta }{2}-a))=\\=underline {2, sinfrac{a}{2}}cdot cos frac{beta -a}{2}cdot 2, sinfrac{beta -a}{2}cdot underline {cosfrac{a}{2}}=sinacdot sin(beta -a); .\\\star ; ; ; sin2x=2, sinxcdot cosx$

Answer 2

cgfc,j

Answer 3

спасбо

Answer 4

помоте пожалуйста https://znanija.com/task/31169390

Answer 5

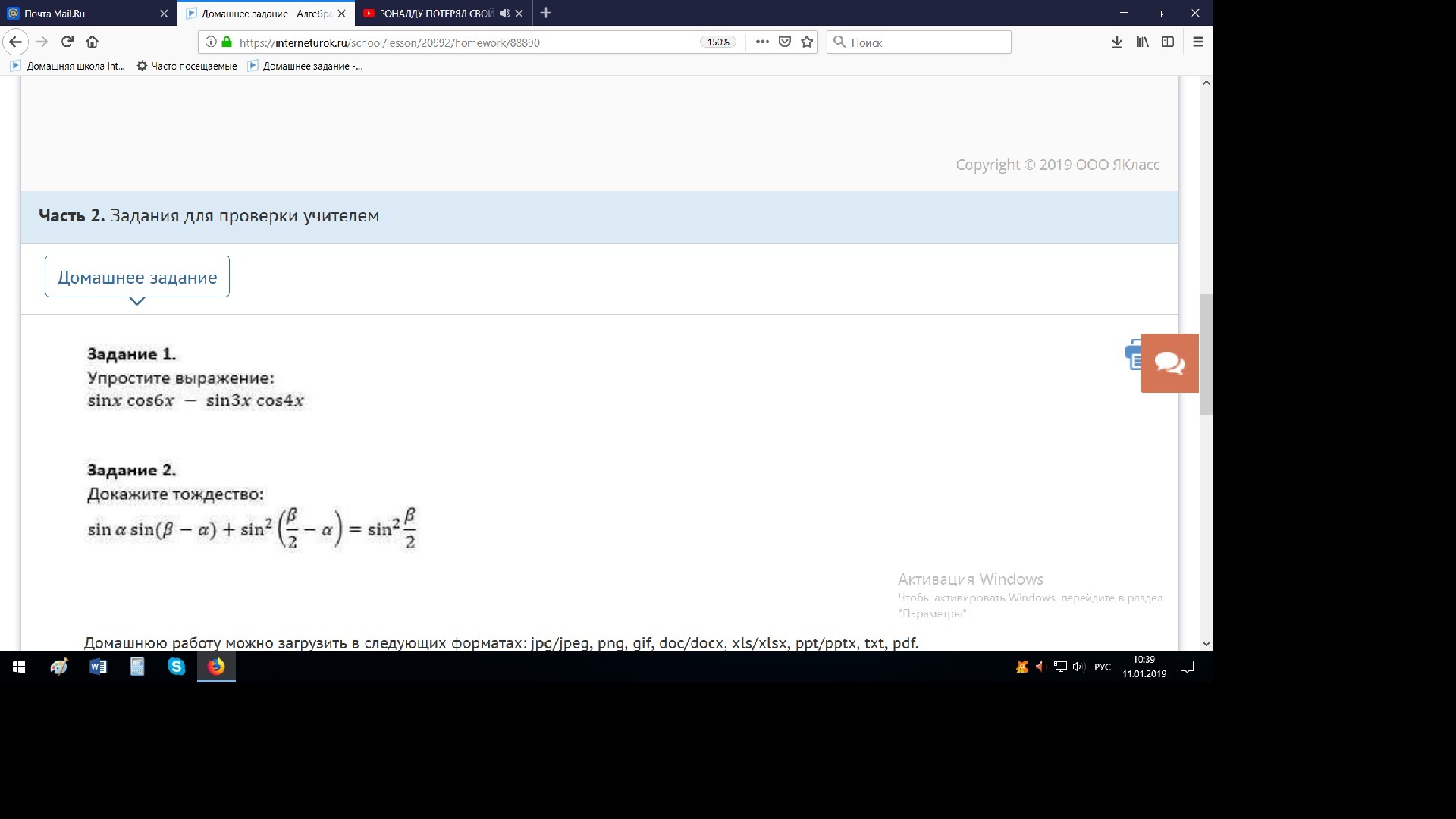
1. =1/2(sin(-5x)+sin7x)-1/2(sin(-x)+sin7x)= -1/2sin5x+1/2sin7x+1/2sinx-1/2sin7x=

1/2(sinx-sin5x)=1/2·2sin(-2x)·cos3x= -sin2x cos3x.  (cм. формулы)

2.рассмотрим левую часть

sinα·sin(β-α)-sin²(β/2-α)=1/2(cos(α-β+α)-cos(α+β-α)+sin²(β/2-α)=

1/2cos(2α-β)-1/2cosβ +1/2-1/2cos(β-2α)=1/2-1/2cosβ=(1-cosβ)/2=sin²(β/2),ч.т.д.

(все по формулам тригонометрии)

Answer 6

спасбо

Answer 7

помоте пожалуйста https://znanija.com/task/31169390