Question

в треугольнике АВС ВС=4,АС=8,АВ=4 корня из 3.Точка Д середина стороны АС. Вычислить площадь треугольника АВД и расстояние от точки А до прямой ВД. дам 20 баллов. ПОЖАЛУЙСТА :)

Answer 1

Определим вид треугольника ABC:

$BC^2+AB^2=4^2+(4sqrt{3})^2=16+48=64\AC^2=8^2=64\AC^2=BC^2+AB^2$

Следовательно ΔABC прямоугольный ∠B = 90°

Найдем площадь ΔABC как полупроизведение катетов:

$S_{ABC}=frac{AB*BC}{2}=frac{4sqrt{3}*4}{2}=8sqrt{3}$

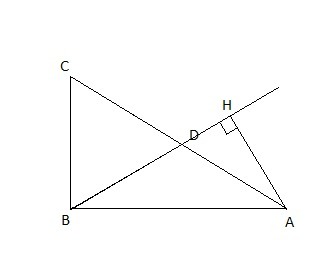
Т.к. D - середина стороны AC, то BD - медиана, которая делит ΔABC на два равновеликих треугольника ⇒

$S_{ABD}=S_{BDC}=frac{1}{2}S_{ABC}=frac{1}{2}*8*sqrt{3}=4sqrt{3}$

Катет BC равен половине гипотенузы AC ⇒ ∠BAC = 30°

Т.к. точка D - середина гипотенузы, то она является центром описанной окружности и BD = AD, а следовательно ΔABD равнобедренный и ∠ABD = ∠BAC = 30°

Расстояние от точки A до прямой BD равно длине перпендикуляра AH, опущенного из этой точки на прямую BD и находится из прямоугольного ΔABH:

$AH=AB*sin{widehat{ABH}}=4sqrt{3}*frac{1}{2}=2sqrt{3}$

Answer 2

большое спасибо