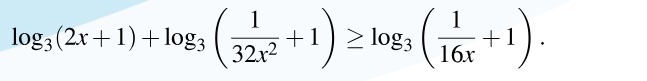Ответы
Ответ дал:
0
{2х+1>0
{1/32х²+1>0
{1/16х+1>0
1)2х>-1;х>-1/2
2)(1+32х²)/32х²>0;х≠0
1+32х²>0;
32х²>0
х€(-оо;0)+(0;+оо)
3)(1+16х)/16х>0;х≠0
16(х+1/16)/(16х)>0
по методу интервалов
__+___-1/16_-___0____+__
х€(-оо;-1/16)+(0;+оо)
1){х€(-1/2;+оо)
2){х€(-оо;0)+(0;+оо)
3){х€(-оо;-1/16)+(0;+оо)
=>х€(-1/2;-1/16)+(0;оо)
____-1/2___-1/16___0_____
{1/32х²+1>0
{1/16х+1>0
1)2х>-1;х>-1/2
2)(1+32х²)/32х²>0;х≠0
1+32х²>0;
32х²>0
х€(-оо;0)+(0;+оо)
3)(1+16х)/16х>0;х≠0
16(х+1/16)/(16х)>0
по методу интервалов
__+___-1/16_-___0____+__
х€(-оо;-1/16)+(0;+оо)
1){х€(-1/2;+оо)
2){х€(-оо;0)+(0;+оо)
3){х€(-оо;-1/16)+(0;+оо)
=>х€(-1/2;-1/16)+(0;оо)
____-1/2___-1/16___0_____
Ответ дал:
0
Вас заинтересует
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад