Question

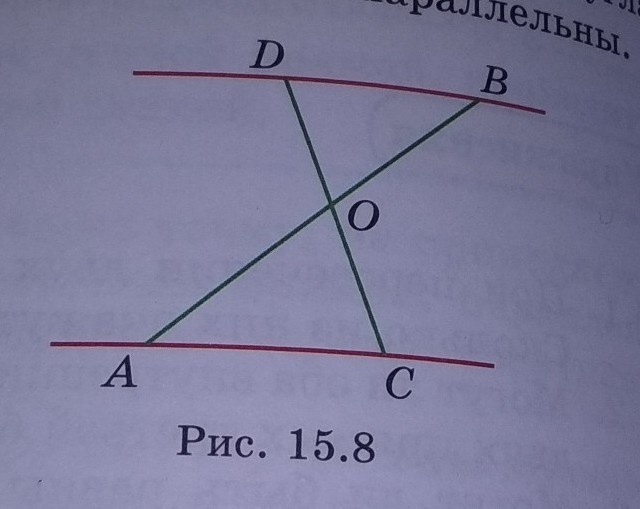
отрезки AB и CD пересекаются в их общей середине о Докажите что прямые AC и BD параллельны

Answer 1

Пусть точка О - общая середина отрезков AB и СD.

Треугольники АОС и ВОD равны за двумя сторонами и углом между ними соотвественно.

(АО=ВО, ОС=ОD - по условию,

угол АОС=угол ВОD - как вертикальные).

Из равенства треугольников следует равенство углов

угол АСО=угол BDO, т.е. то же самое, что

угол ACD=угол BDC

угол ACD и угол BDC - внутренние разносторониие углы при прямых АС и BD и секательной CD. Поэтому по теореме прямые АС и BD параллельны. Доказано

Надеюсь помогла.

Answer 2

Рассмотрим ∠BDO и ∠CDO.

AO = OB, CO = OD.

∠COA = ∠DOB (Вертикальные)

Значит: ∠AOC = ∠BOD по 1 признаку ⇒ ∠1 = ∠2, а т.к. ∠А = ∠В - накрест лежащих при прямых AC, BD и Секущей AB, то AC║BD