Question

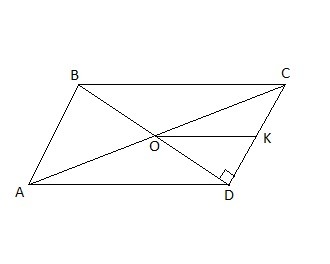
В параллелограмме ABCD диагональ BD перпендикулярна стороне CD, угол C=60* . Прямая, проходящая через точку O, параллельна AD и пересекает сторону CD в точке K. Найдите площадь параллелограмма ABCD, если OK=6см.

Answer 1

Т.к. OK ║ AD, а AD ║ BC ⇒ OK ║ BC

Точка O - центр пересечения диагоналей параллелограмма делит их пополам ⇒ OK средняя линия ΔBCD.

BC = 2 * OK = 2 * 6 = 12 см

В прямоугольном ΔBCD ∠CBD = 90° - ∠BCD = 90° - 60° = 30°.

Против угла в 30° лежит половина гипотенузы ⇒ CD = BC / 2 = 12 / 2 = 6.

В прямоугольном ΔBCD по теореме Пифагора найдем:

$BD=sqrt{BC^2-CD^2}=sqrt{12^2-6^2}=sqrt{6*18}=6sqrt{3}$

Площадь прямоугольного ΔBCD найдем как полупроизведение катетов:

$S_{BCD}=frac{CD*BD}{2}=frac{6sqrt{3}*6}{2}=18sqrt{3}$

Т.к. диагональ BD делит параллелограмм на два равных треугольника, то:

$S_{ABCD}=2*S_{BCD}=2*18*sqrt{3}=36sqrt{3}$

Ответ: площадь параллелограмма равна 36√3 см2

Answer 2

А можно без sin,cos т.к ещё этого не проходили.