Question

Найти площадь фигуры ограниченной линиями y=6x-x² и y=o

Answer 1

у = y = 6x-x²;

у = 0

S = ?

Решение

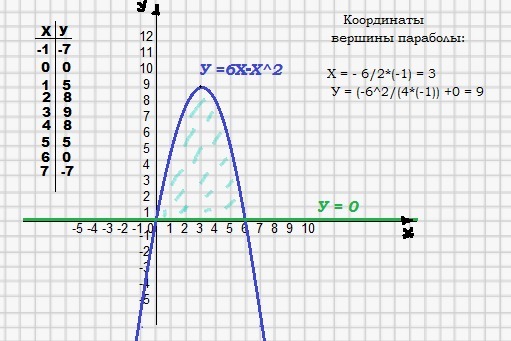
y = 6x-x²  - парабола с ветвями, обращенными вниз, у = 0 - прямая, проходящая по оси абсцисс.

6х - х² = 0;  х(х-6) = 0 ; х₁ = 0 и х₂= 6 ---- точки пересечения параболы у = 6=х² с прямой у = 0

    Площадь фигуры, ограниченной линиями заданных функций,находится с помощью определенного интеграла, пределы интегрирования 0 и 6

$displaystyle intlimits^6_0 {(6x-x^{2} )} , dx=(3x^{2} -frac{x^{3} }{3})|_{o} ^{6} =3*6^{2}-frac{6^{3} }{3} -3*0^{2}+frac{0^{3} }{3}=\ 3*36-frac{216}{3}=108-72=36$

Ответ:  36