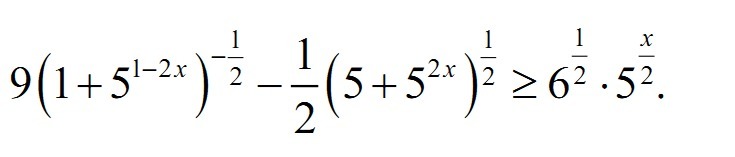Question

помогите решить неравенство, плиииз!!!!

Answer 1

$displaystyle 9(1+5^{1-2x})^{-frac{1}{2}}-frac{1}{2}(5+5^{2x})^{frac{1}{2}}geq 6^{frac{1}{2}}*(5^x)^{frac{1}{2}}\\9(1+frac{5}{5^{2x}})^{-frac{1}{2}}-frac{1}{2}(5+5^{2x})^{frac{1}{2}}geq sqrt{6}*(5^x)^{frac{1}{2}}\\9(frac{5^{2x}}{5^{2x}+5})^{frac{1}{2}}-frac{1}{2}(5+5^{2x})^{frac{1}{2}}geq sqrt{6}*(5^x)^{frac{1}{2}}| : (5^x)^{frac{1}{2}}\\9(frac{5^x}{5^{2x}+5})^{frac{1}{2}}-frac{1}{2}(frac{5+5^{2x}}{5^x})^{frac{1}{2}}geq sqrt{6}$

$displaystyle(frac{5^x}{5^{2x}+5})^{frac{1}{2}}=t$

$displaystyle 9t-frac{1}{2t}geq sqrt{6}\\frac{18t^2-2sqrt{6}t-1}{2t}geq 0\\18t^2-2sqrt{6}t-1=0\\D=4*6+4*18=96=(4sqrt{6})^2\\t_{1.2}=frac{2sqrt{6}pm 4sqrt{6}}{36}\\t_1=frac{sqrt{6}}{6}; t_2=-frac{sqrt{6}}{18}$

$displaystyle frac{18(t-frac{sqrt{6}}{6})(t+frac{sqrt{6}}{18})}{2t}geq 0$

решаем методом интервалов

_______ -√6/18________0_______√6/6_______

     <0                         >0             <0                       >0

$displaystyle -frac{sqrt{6}}{18}leq t<0; tgeq frac{sqrt{6}}{6}$

делаем обратную замену

$displaystyle -frac{sqrt{6}}{18}leq (frac{5^x}{5^{2x}+5})^{frac{1}{2}}<0$

решений нет

$displaystyle (frac{5^x}{5^{2x}+5})^frac{1}{2}geqfrac{sqrt{6}}{6}\\frac{5^x}{5^{2x}+5}geq frac{1}{6}\\frac{6*5^x-5^{2x}-5}{6(5^{2x}+5)}geq 0\\ 5^x=a\\frac{-(a^2-6a+5)}{6(a^2+5)}geq 0$

Знаменатель для любых а положителен

$displaystyle -(a^2-6a+5)geq 0\\-(a-1)(a-5)geq 0\\1leq aleq 5\\1leq 5^xleq 5\\0leq xleq 1$

Ответ [0;1]