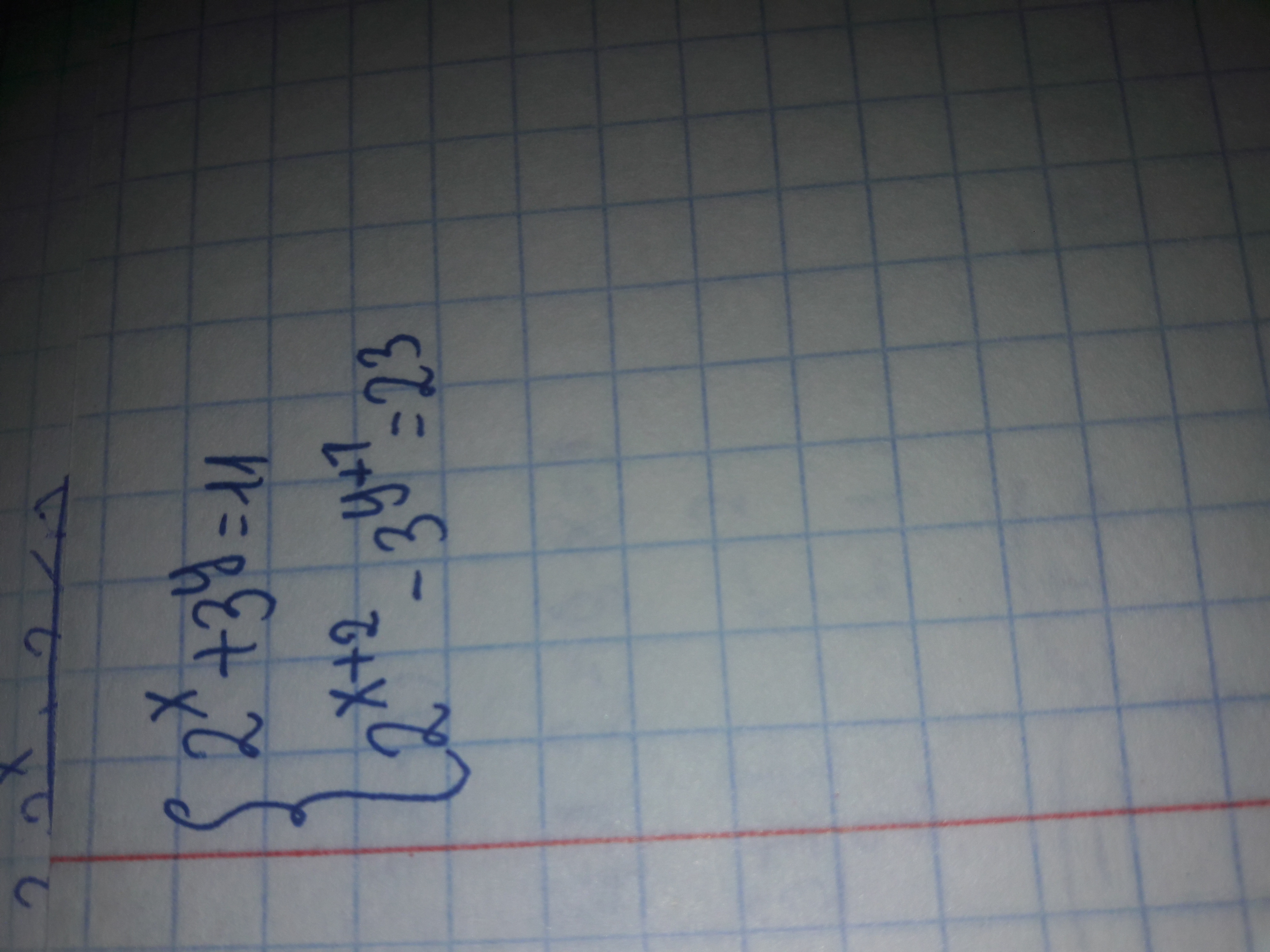Question

Помогите решить показательные уравнение

Answer 1

$2^x=11-3^y\2^{x+2}=(11-3^y)*4=44-4*3^y\2^{x+2}-3^{y+1}=23\44-4*3^y-3^{y+1}=23\3^y(4+3)=21\3^y=3\y=1\2^x=11-3^1=8\x=3$

Answer 2

Спасибо вам! Очень благодарна! Но не могу понять почему умножили 11-3^у на 4?)

Answer 3

Это я верхнее равенство домножил на 2^2 = 4. Левая часть стала 2^x * 2^2 = 2^(x+2), а правая как уже написано

Answer 4

Спасибо!

Answer 5

2x=11−3y
2x+2=(11−3y)∗4=44−4∗3y
2x+2−3y+1=23
44−4∗3y−3y+1=23
3y(4+3)=21
3y=3
y=1
2x=11−31=8
x=3​