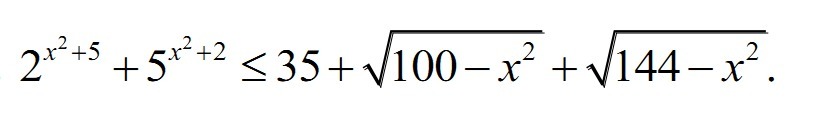Ответы
Ответ дал:
0
На самом деле это решается устно, но можно всё расписать:
Найдем область значения левой и правой части неравенства:
Любое число в квадрате больше либо равно нулю


Получается, что левая часть исходного неравенства всегда ≥57, а правая часть при любом "х" ≤57, следовательно данное неравенство будет равносильно уравнению:

И равенство может быть достигнуто только если обе части будут равняться 57, это достигается при наименьшем значении левой части при х=0 и при наибольшей правой (также при х=0)
Ответ: х=0
Найдем область значения левой и правой части неравенства:
Любое число в квадрате больше либо равно нулю
Получается, что левая часть исходного неравенства всегда ≥57, а правая часть при любом "х" ≤57, следовательно данное неравенство будет равносильно уравнению:
И равенство может быть достигнуто только если обе части будут равняться 57, это достигается при наименьшем значении левой части при х=0 и при наибольшей правой (также при х=0)
Ответ: х=0
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
10 лет назад