корни х1 и х2 уравнения 2х^2+kх+7=0 удовлетворяют условию х1/х2 + х2/х1= 36/7. Найдите значение k. Помогите пожалуйста
Приложения:
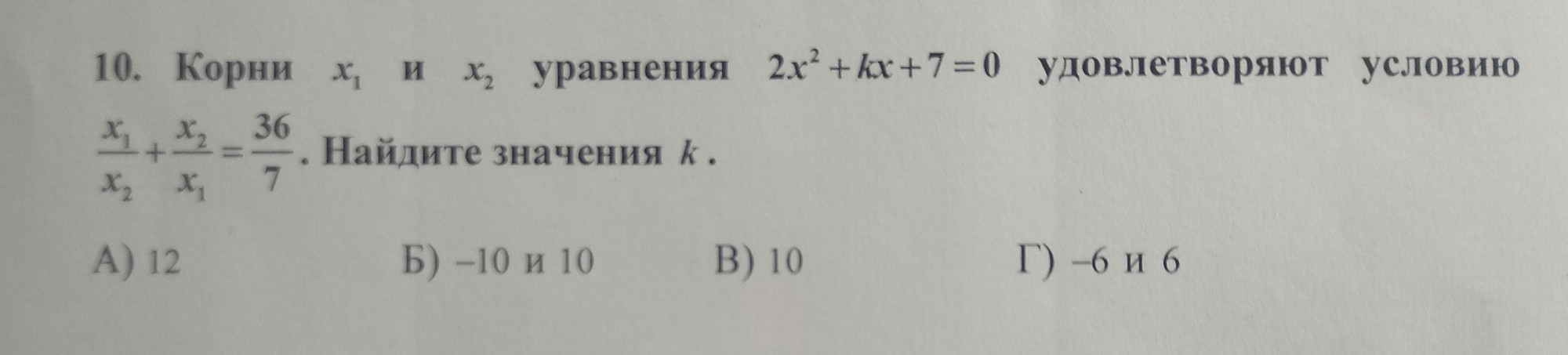
Ответы
Ответ дал:
0
Преобразуем выражение:
А теперь применим теорему Виета:
Вас заинтересует
3 года назад
3 года назад
9 лет назад
10 лет назад