Ответы
Ответ дал:
0
.....????????????......
Приложения:

Ответ дал:
0
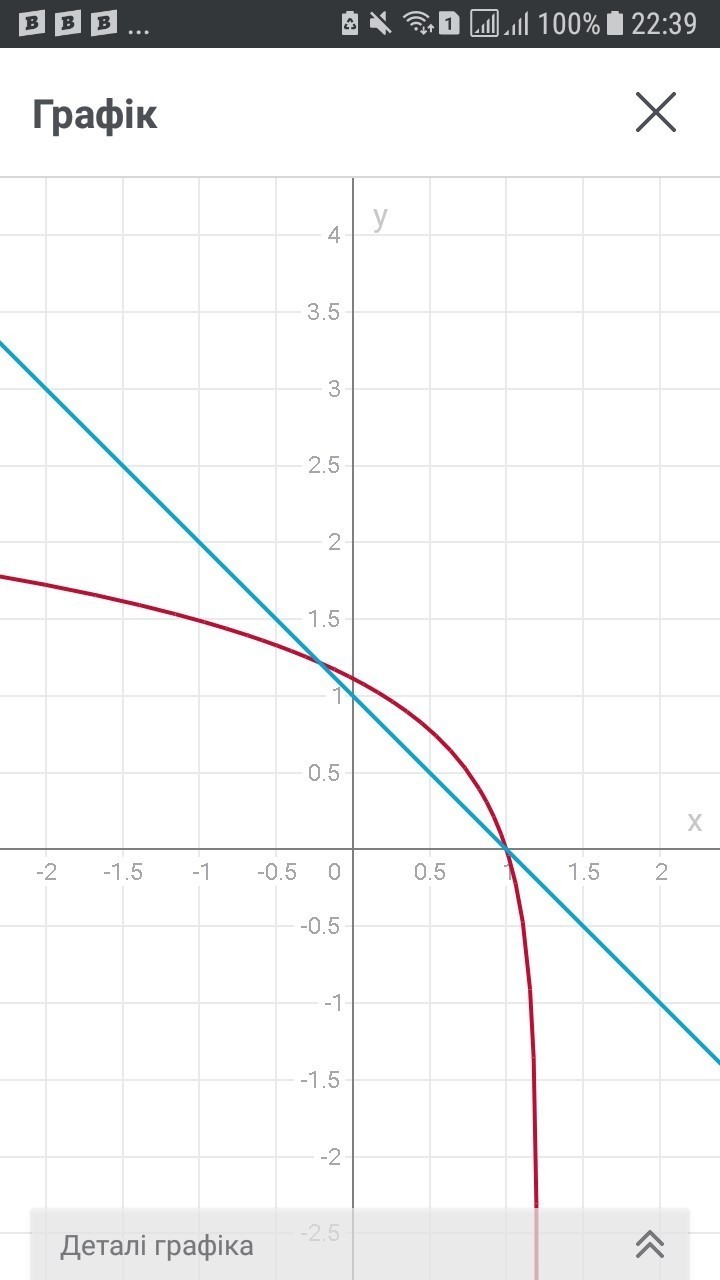
уравнение нужно решить ( без графика
Ответ дал:
0
ОДЗ:
6 - 5^x > 0 -- оба корня подходят
Ответ: 0; 1
Приложения:


Ответ дал:
0
спасибо огромное ❤️
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад