Question

В треугольнике ABC угол C=90°, AC=9 см, AB+BC=27 см. Найдите гипотенузу AB.

Answer 1

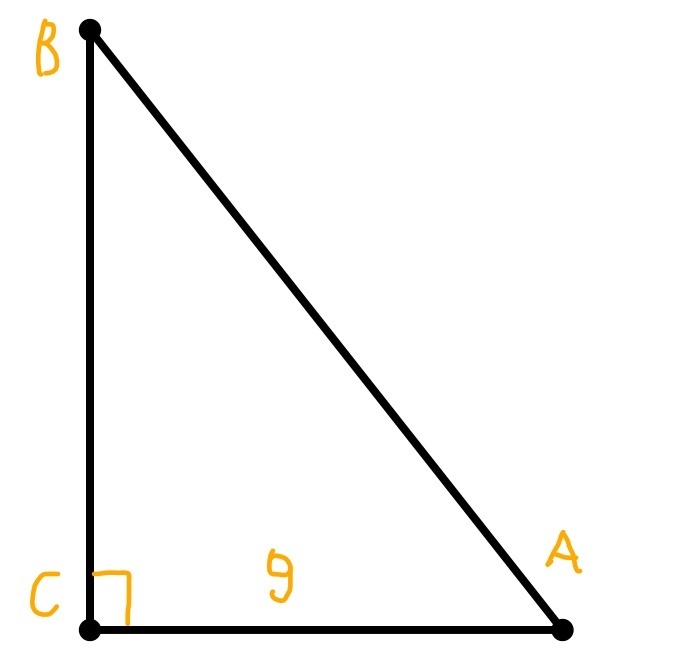
AC - катет

Выразим его через AB и CB по теореме Пифагора:

AB² - BC² = AC²

AB² - BC² = 81

Составим систему и решим её

$left {begin{array}{lcl} {{AB^2-BC^2=81} \ {AB+BC=27} end{array}}right. \\left {begin{array}{lcl} {{(AB-BC)(AB+BC)=81} \ {AB+BC=27} end{array}}right.\\left {begin{array}{lcl} {{(AB-BC)cdot 27=81} \ {AB+BC=27} end{array}}right. \\left {begin{array}{lcl} {{AB-BC=3} \ {AB+BC=27} end{array}}right.\\left {begin{array}{lcl} {{AB-BC+(AB+BC)=3+27} \ {AB+BC=27} end{array}}right.\ \left {begin{array}{lcl} {{2AB=30} \ {AB+BC=27} end{array}}right.$

$left {begin{array}{lcl} {{AB=15} \ {BC=12} end{array}}right.$

Ответ: 15

Answer 2

Можно так: по Пифагору 81+(27-АВ)^2=АВ^2 => 54*АВ=81+729 => АВ = 15.