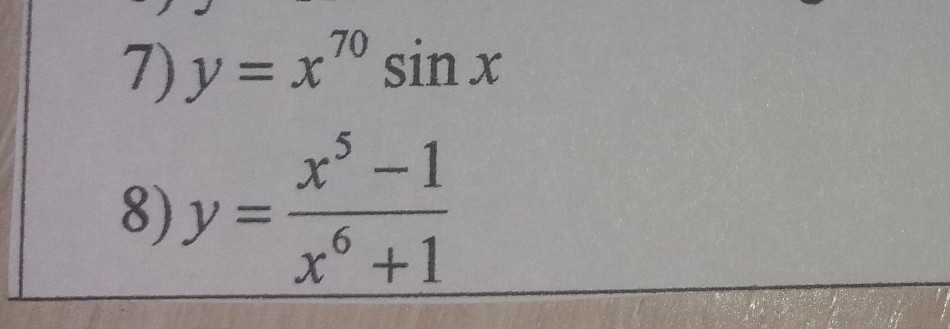Ответы
Ответ дал:
0
7) y=x⁷⁰*sin(x)
y'=(x⁷⁰)'*sin(x)+x⁷⁰*(sin(x))'=70*x⁶⁹*sin(x)+x⁷⁰*cos(x)=
=x⁶⁹*(70*sin(x)+x*cos(x)).
8) y=(x⁵-1)/(x⁶+1)
y'=((x⁵-1)'*(x⁶+1)-(x⁵-1)*(x⁶+1))/(x⁶+1)²=(5x⁴*(x⁶+1)-6x⁵*(5x-1))/(x⁶-1)²=
=(x⁴*(5*(x⁶+1)-6x*(x⁵-1))/(x⁶+1)²=x⁴*(5x⁶+5-6x⁶+6x)/(x⁶+1)²=
=x⁴*(-x⁶+6x+5)/(x⁶+1)².
Ответ дал:
0
Спасибо :3
Ответ дал:
0
Удачи.
Ответ дал:
0
Ответ дал:
0
Спасибо :3
Вас заинтересует
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад