Решите хотя бы одно уравнение плиз!!!!!
1) cos^2(x) - sin(2x) = 1
2) 9^(log3lg(x))=log(x)-2lg^2+4
Приложения:
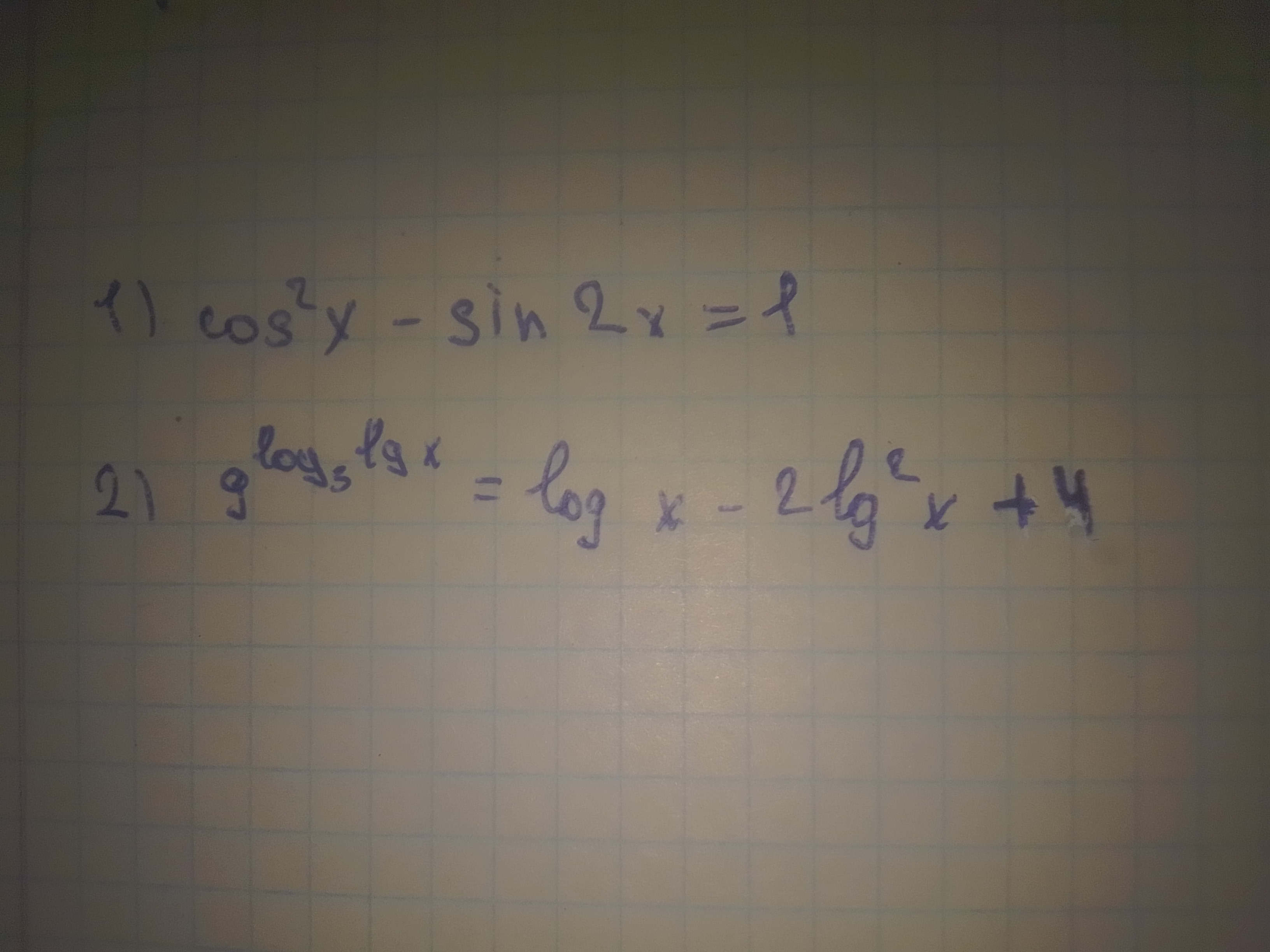
Ответы
Ответ дал:
0
1) сos²x - sin2x = 1;
cos²x - 2sinx·cosx = cos²x + sin²x
sin²x + 2sinx · cosx = 0
sinx · (sinx + 2cosx) = 0
1) sinx = 0; x₁ = πk (k∈Z)
2) sinx + 2cosx = 0
cosx ≠ 0
tgx + 2 = 0
tgx = -2
x₂ = - arctg(2) + πk (k∈Z)
x = πk (k∈Z)
2) 9^(log₃ (lgx)) = lgx - 2lg²x + 4
ОДЗ: х > 0; lgx > 0;
3^(2log₃(lgx)) = lgx - 2lg²x + 4
3^(log₃ (lg²x)) = lgx - 2lg²x + 4
lg²x = lgx - 2lg²x + 4
3lg²x - lgx - 4 = 0
Замена t = lgx
3t² - t - 4 = 0
D = 1 + 48 = 49
t₁ = (1 - 7)/6 = -1 ; -1 = lgx; не подходит из-за ОДЗ
t₂ = (1 + 7)/6 = 8/6 = 4/3; 4/3 = lgx; x₂ = 10^4/3 = 10∛10
Ответ: х = 10∛10 или х = ∛10 000, что одно и то же
Ответ дал:
0
Там синус не степень а 2х
Ответ дал:
0
Я исправила
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад