Question

Докажите, что медиана треугольника меньше половины его периметра. Если можно, с картинкой..

Answer 1

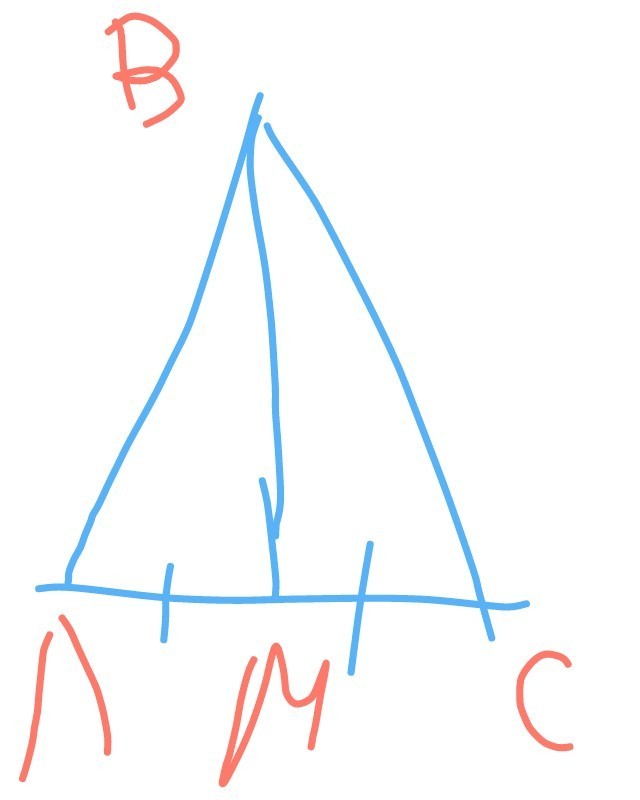
После деления медианной BM треугольника АВС образовались два треугольника: АВМ и СВМ,
У треугольника каждая сторона всегда меньше, чем сумма двух остальных.
Нас интересует неравенство с ВМ в левой части.
Следовательно, ВМ<АМ+АВ,
ВМ<СВ+СМ.
Сложим эти неравенства:
2ВМ<АВ+ВС+АМ+СМ
АМ и СМ в сумме дают сторону АС.
Итого:
2ВМ<Р
ВМ<P/2
Доказано.

Answer 2

Я почти так же написала, спасибо)

Answer 3

Не за что)