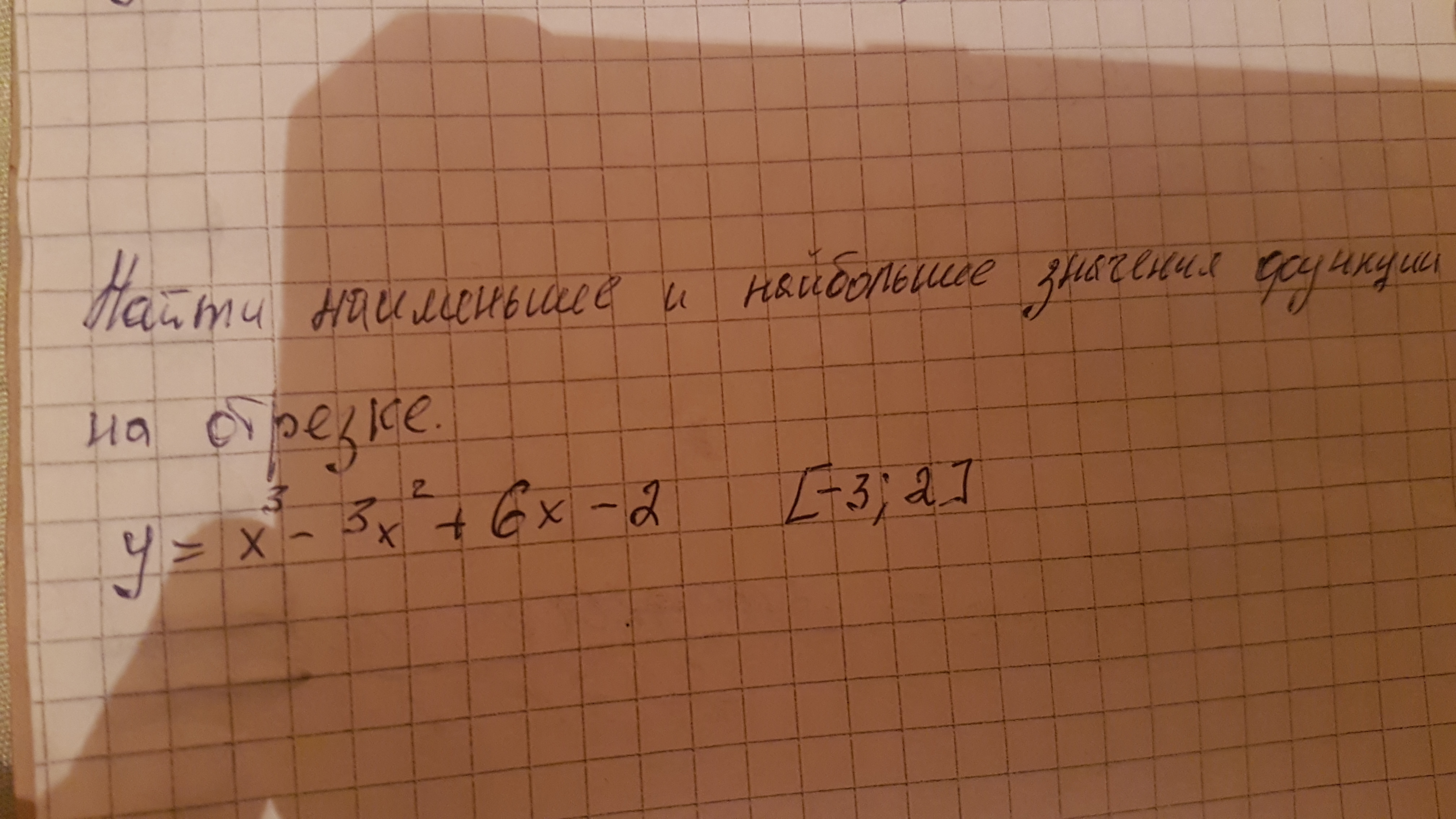Question

Уважаемые, помогите решить, срочно нужно. Давно это изучал и не очень помню уже.

Answer 1

$sf y=x^3-3x^2+6x-2$

Находим производную

$sf y'=3x^2-6x+6$

Находим стационарные точки

$sf 3x^2-6x+6=0 \ x^2-2x+2=0 \ frac{D}{4}=1-2=-1<0$

Стационарные точки отсутствуют. Производная принимает только положительные значения, а значит функция монотонно возрастает.

$sf y_{min[-3; 2]}=y(-3)=-27-27-18-2=-74 \ y_{max[-3; 2]}=y(2)=8-12+12-2=6$

Ответ: -74 - минимальное значение, 6 - максимальное значение

Answer 2

Спасибо тебе, добрый человек))