Question

ПОМОГИТЕ ДА. 70 БАЛОВ!!!!!!!!! СРОЧНООО

площадь основания правильной четырехугольной пирамиды равна площади сечения, проходящей через высоту и диагональ основания. Найти объем пирамиды, если ее высота равна Н = ∛12

Answer 1

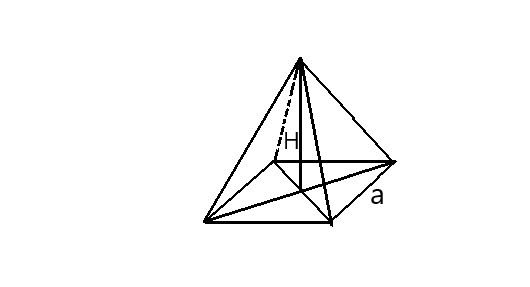
Сечение проходящее через высоту и диагональ основания правильной четырехугольной пирамиды - равнобедренный треугольник с высотой Н и основанием а√2, где а - сторона основания пирамиды. Площадь сечения - S=(a√2*∛12)/2=a². ⇒           а=(√2*∛12)/2 - сторона основания правильной четырехугольной пирамиды. Sосн=а²=(2∛12*∛12)/4, V=S(осн)*H/3=(2∛12*∛12*∛12)/(4*3)=2*12/12=2 ед³.