Question

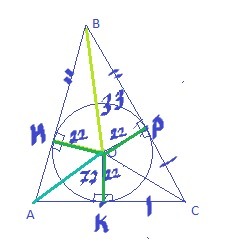
Радиус окружности, вписанной в треугольник ABC, равен 22 см. Расстояние от центра О этой окружности до вершин A и B равны OA=77см, OB=33см. Найти расстояние OC.

Answer 1

1)Найдём BP и AK по теореме Пифагора:

BP=√BO²-OP²=√33²-22²=11√5

AK=√AO²-OK²=√77²-22²=33√5

Отсюда можно найти AB=33√5+11√5=44√5

2)Заметим, что BH=BP(как отрезки касательных,проведённых из одной точки)

Вспомним, что центр вписанной окр.-точка пересечения биссектрис треугольника, поэтому найдём синус угла ABC, используя этот факт:

sin2α=2sinαcosα=2*$frac{OH}{BO} *frac{BH}{BO}$=$frac{4sqrt{5} }{9}$

Пусть CP=CK=x,

Тогда SΔ=$frac{4sqrt{5} }{9} *frac{1}{2} *44sqrt{5} *(11sqrt{5} +x)=frac{88*5}{9}( 11sqrt{5} +x)$    

С другой стороны, SΔ=S(ABO)+S(AOC)+S(BOC)

SΔ=$22*frac{1}{2} *44sqrt{5} +22*frac{1}{2}*(33sqrt{5}+x) +22*frac{1}{2}*(11sqrt{5} +x)=\11(2x+88sqrt{5} )$

Приравнивая два вышенаписанных выражения для площади, найдём, что x=16$sqrt{5}$.

3)Тогда CO можно найти по теореме Пифагора:

CO=√OK²+CK²= √196*9=42            

Answer 2

делал не так : через tg (C/2) , ответ такой - же

Answer 3

Разумеется,есть несколько методов решения

Answer 4

У вас хорошее решение ( через площадь ) , мне понравилось , найти короткое без синусов ( тригонометрии) не получилось , хотя может быть его и нет

Answer 5

                Решение : /////////////////////////////////////