ГЕОМЕТРИЯ
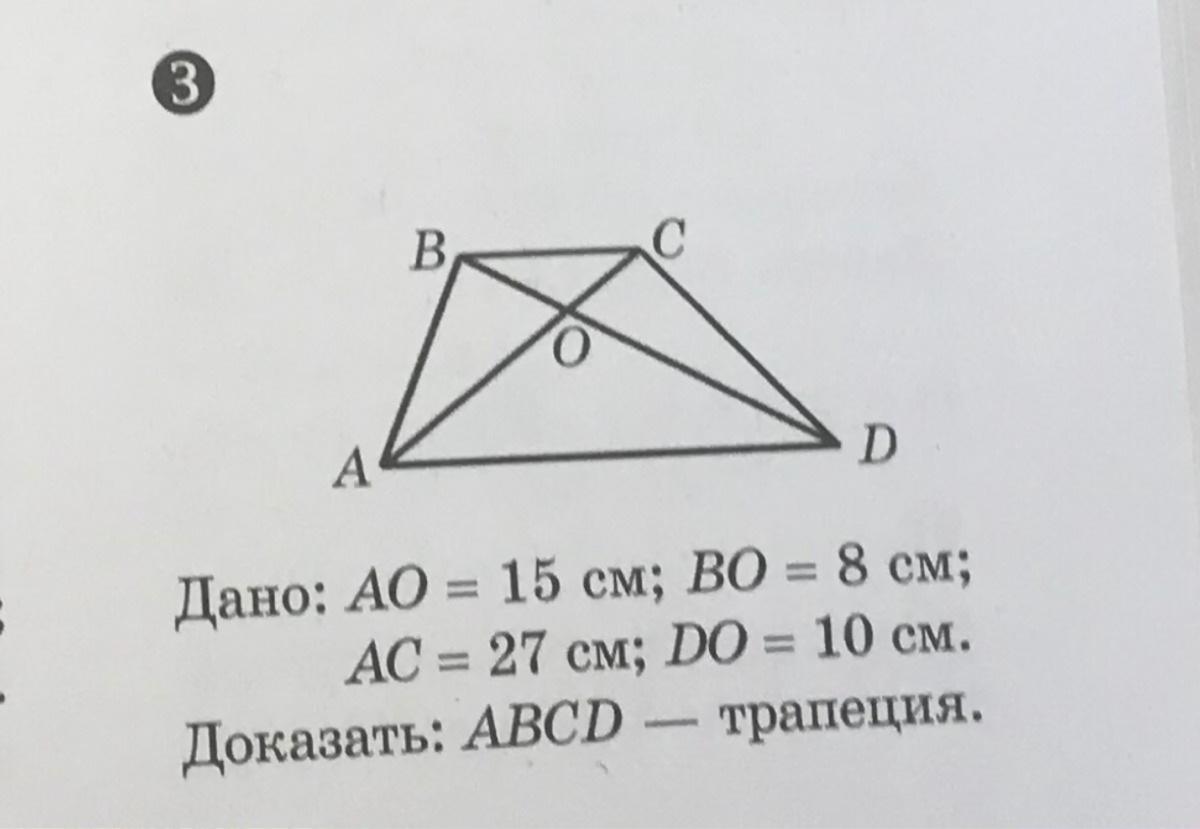
AO=15, BO =8
AC = 27, DO=10
Доказать,что ABCD трапеция, используя признаки подобия треугольников
Приложения:
Ответы
Ответ дал:
0
BOC подобен AOD по углу и двум пропорциональным сторонам(BOC=AOD - вертикальные углы и BO/OD = OC(12)/AO). Из подобия треугольников следует равенство соответственных углов и ропорциональность сходственных сторон,значит BCO = CAD(нлу при прямых линий BC,AD и секущей AC),а отсюда следует,что BC||AD и по определению трапеции получается,что четырёхугольник ABCD - трапеция,ведь 2 стороны параллельны,а две другие не параллельны
Ответ дал:
0
ВОС и AOD подобны (по второму признаку)
Следовательно ВСО равен DAO
Эти углы будут внутренними накрест лежащими углами
А значит, ВС параллельно AD
Следовательно ABCD-трапеция
Следовательно ВСО равен DAO
Эти углы будут внутренними накрест лежащими углами
А значит, ВС параллельно AD
Следовательно ABCD-трапеция
Вас заинтересует
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад