Question

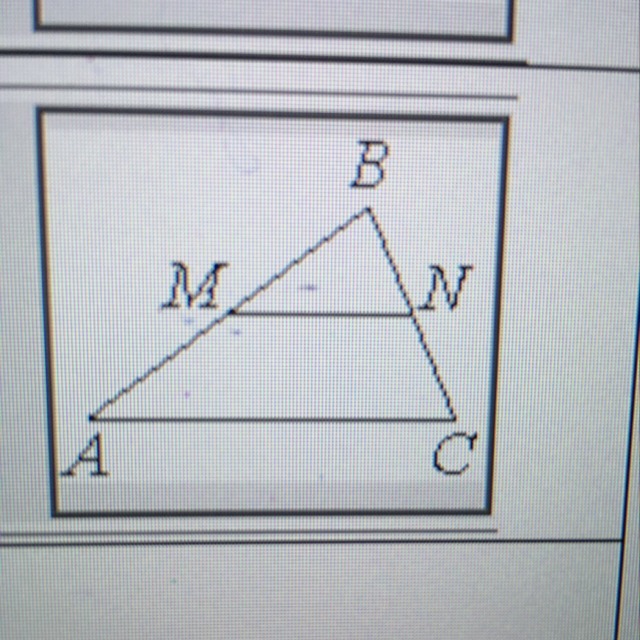
Прямая, параллельная стороне AC треугольника ABC, пересекает стороны AB и BC в точках M и N соответственно, AB= 9, AC=18,MN=14. Найти AM

Answer 1

Т.к. МN параллельно АС треугольник МВN подобен треугольнику АВС, так что AC/MN=АВ/МВ=ВС/ВN=k(k- коэффициент подобия). Отсюда коэффициент подобия= АС/МN и равен 18/8=9/4. Отсюда МВ=АВ/k и равен 9/(9/4)=4. Но АМ= АВ-МВ, отсюда следует что АМ=9-4=5. Ответ: искомая сторона равна 5

Answer 2

Если Mn=8

Answer 3

Я исправил