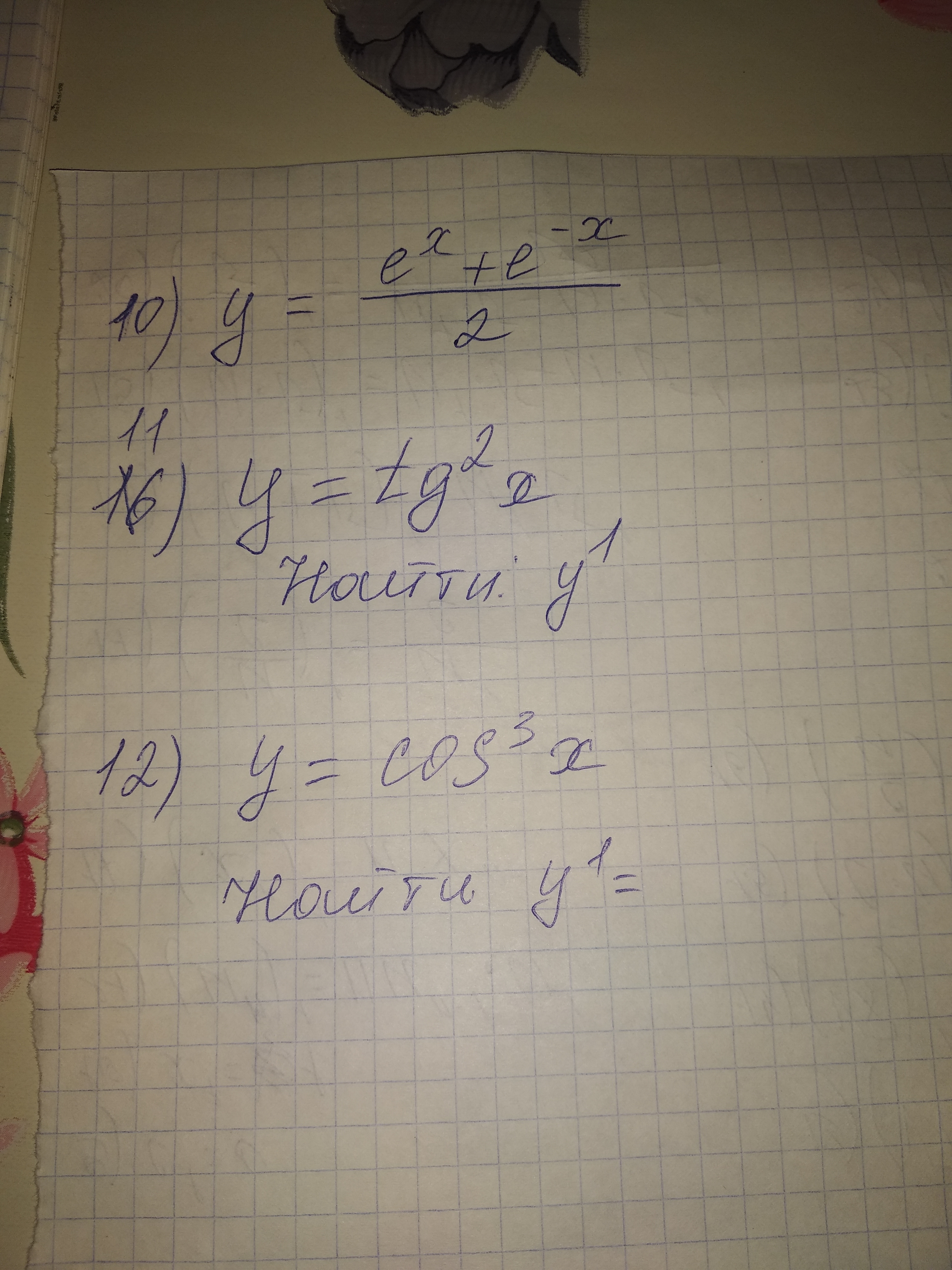Question

Пожалуйста помогите
Желательно с формулами

Answer 1

Универсальная формула подходящая для решения большинства задач на производные: $(x^{n} )'=nx^{n-1}$

${{left( uleft( x right)cdot vleft( x right) right)}^{prime }}={u}'left( x right)vleft( x right)+uleft( x right){v}'left( x right)$

1) $y'=(3x)'=3$

2) $y'=(frac{1}{x^{2} } )'=(x^{-2} )'=-frac{2}{x^{3} }$

3) $y'=(frac{3}{x^{4} } )'=(3x^{-4} )'=-frac{12}{x^{5} }$

4) $y'=(frac{1}{2sqrt{x} } )'=frac{1}{2} *(x^{-frac{1}{2} } )'=-frac{1}{4} *x^{-frac{3}{2} } = -frac{1}{4xsqrt{x} }$

5) ${{left( frac{uleft( x right)}{vleft( x right)} right)}^{prime }}=frac{{u}'left( x right)vleft( x right)-uleft( x right){v}'left( x right)}{{{v}^{2}}left( x right)}, vleft( x right)ne 0$ (решишь сам по аналогии, просто времени нет расписывать)

6) $y'=(3sin,x)'=3cos,x$, так как $(sin,x)'=cos,x$

7) $y'=(e^{-x} )'=-e^{-x}$, так как $(e^{kx+b} )'=ke^{kx+b}$

8) $y'=(sqrt{1-x} )'=-frac{1}{2sqrt{1-x} }$

9) $y' =(2sin, x,cos,x)'= 2cos^2x- 2sin^2x=2cos,2x$

10)${{left( frac{uleft( x right)}{vleft( x right)} right)}^{prime }}=frac{{u}'left( x right)vleft( x right)-uleft( x right){v}'left( x right)}{{{v}^{2}}left( x right)}, vleft( x right)ne 0$ (решишь сам по аналогии, просто времени нет расписывать)

11) $y'=(tg^2x)'=2tg^{2-1}xcdot (tg x)'=2tgxcdot dfrac{1}{cos^ 2x} =dfrac{2tgx}{cos^ 2x}$

12) $y'= (cos^{3} x)'= =-3cos^2x*sin,x$