Question

ГЕОМЕТРИЯ, 25 БАЛЛОВ!!!! Решить задачу расписывая на дано, найти, решение
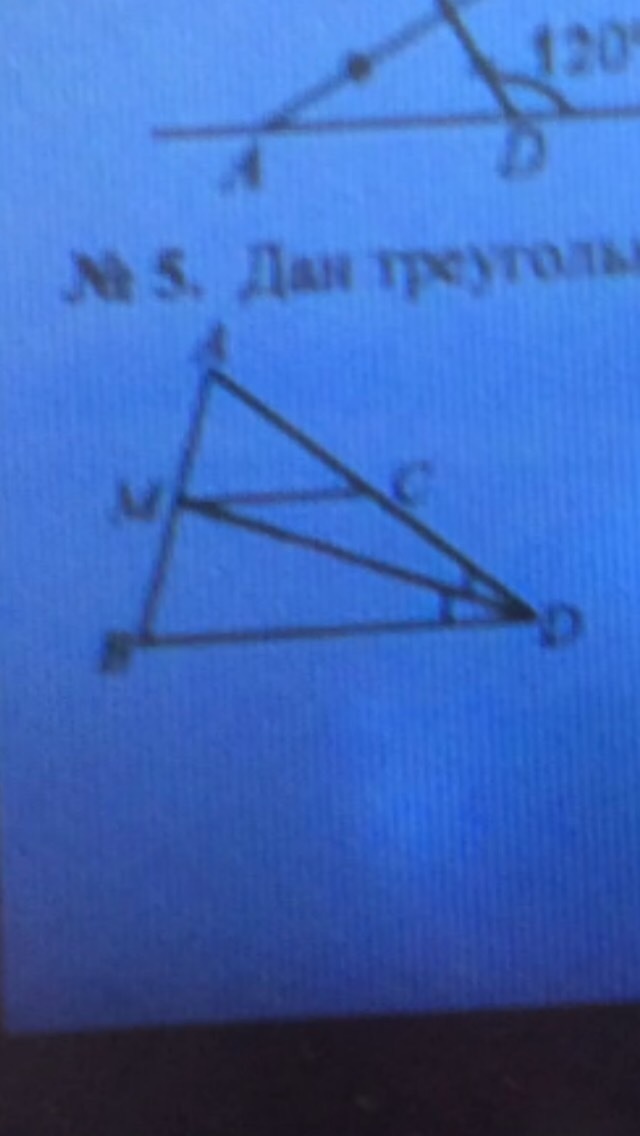
Дан треугольник ADB. На стороне AB взята точка M, а на стороне AD - точка C, так что прямые MC и BD параллельны. DM - биссектриса ∠ADB. ∠CMD=33°. Найдите ∠MCD!!(рисунок треугольника на фото)

Answer 1

Дано:

ΔABD ; MD биссектриса ; MC║BD

∠CMD=33°

Найти:

∠MCD

Решение:

∠CMD=∠MDB так как они накрест лежащие при параллельных прямых MC и AD и секущей MD.

Раз ∠CDM=∠MDB по условию, то ∠CDM=∠CMD=33°

Тогда ∠MCD=180°-∠CDM-∠CMD=180°-33°-33°=114°

Answer 2

В описании же написано, что надо сделать расписывая задачу на "дано" и "найти"

Answer 3

у меня так и сделано

Answer 4

надо было страницу обновить

Answer 5

))))

Answer 6

Пометь ответ как лучший если не сложно)

Answer 7

А подскажи что во 2 пункте написано в скобочках)

Answer 8

Накрест лежащие при параллельных прямых MC и BD и секущей MD)

Answer 9

Пасиб