Помогите пожалуйста решить одно логарифмическое выражение! Даю 50 баллов! Задание на фото. Спасибо большое за помощь!
Приложения:
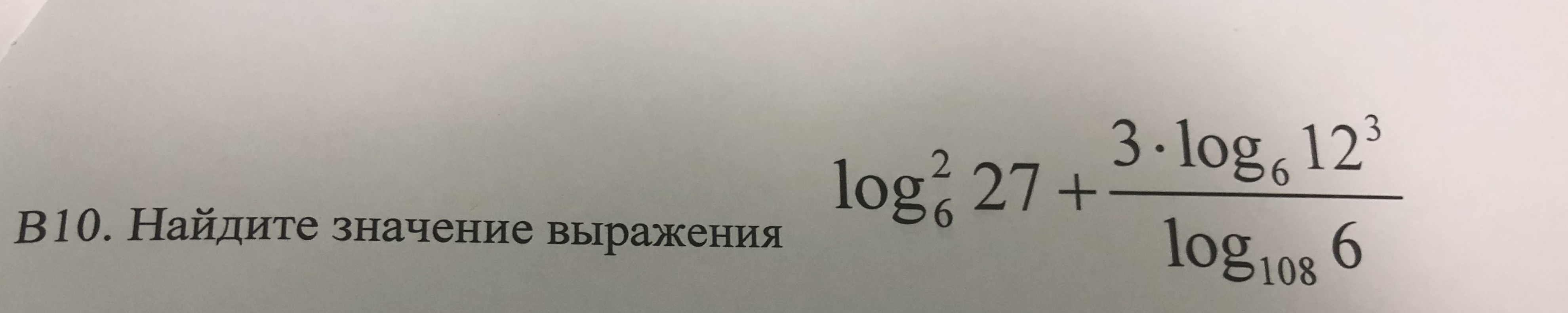
Ответы
Ответ дал:
0
Ответ дал:
0
Спасибо огромное!))
Ответ дал:
0
Пожалуйста
Ответ дал:
0
Ответ 36. Решение задания приложено.
Приложения:
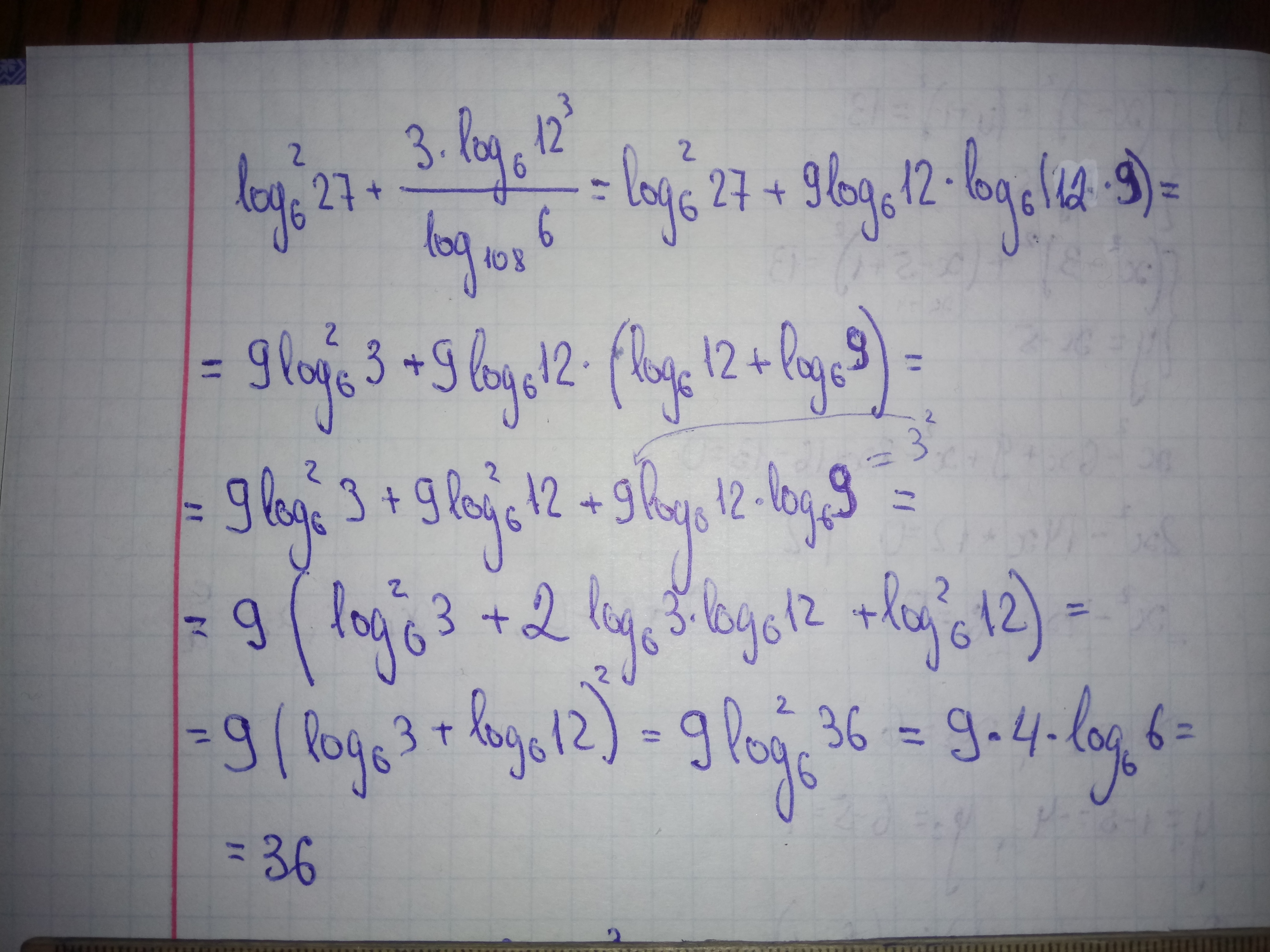
Ответ дал:
0
Другой путь
Вас заинтересует
2 года назад
2 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад