Ответы
Ответ дал:
0
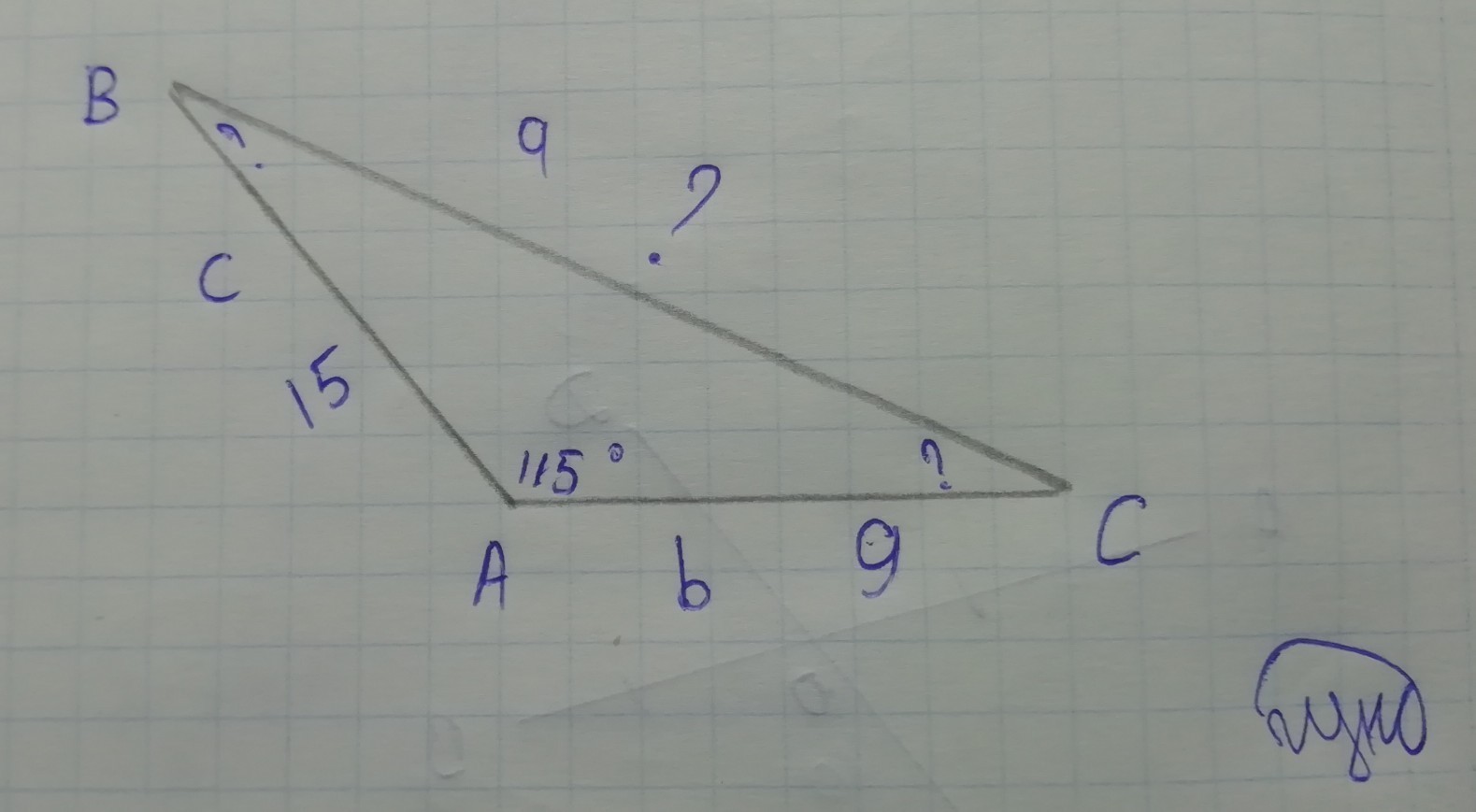
Используем теорему косинусов

Подставляем

Далее используем теорему синусов

Подставляем

Синус в 0.67 есть угол в ≈ 42°
Т. е. ∠C ≈ 42°
∠B = 180 - 115 - 42 ≈ 23° (сумма углов треугольника равна 180°)
Ответ: a ≈ 20,5; ∠C ≈ 42°; ∠B ≈ 23°.
Подставляем
Далее используем теорему синусов
Подставляем
Синус в 0.67 есть угол в ≈ 42°
Т. е. ∠C ≈ 42°
∠B = 180 - 115 - 42 ≈ 23° (сумма углов треугольника равна 180°)
Ответ: a ≈ 20,5; ∠C ≈ 42°; ∠B ≈ 23°.
Приложения:
Вас заинтересует
2 года назад
3 года назад
3 года назад
9 лет назад
9 лет назад
10 лет назад